Глава 2. Угол
2.3. Различные виды углов
Два угла называются
смежными, если у них одна сторона общая, а другие стороны являются дополнительными лучами.
 1
|
| Рисунок 2.3.1. Смежные углы
|
Легко доказать следующие теоремы о смежных углах:
Угол называется
прямым, если его величина равна
90°. Угол, меньший
90°, называется
острым; больший
90°, но меньший
180° –
тупым.
 2
|
| Рисунок 2.3.2. Различные виды углов
|
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого угла.
 3
|
| Рисунок 2.3.3. Вертикальные углы
|
Теорема о сумме смежных углов позволяет доказать, что вертикальные углы равны.
Пусть прямые a и b пересекаются в точке A. Точка A разбивает каждую прямую на два взаимно дополнительных луча с вершиной в точке A.
Определение 2.1.
Углом между прямыми a и b называется меньший из углов с вершиной в точке A сторонами которого являются пара лучей, принадлежащих разным прямым.
Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Для обозначения перпендикулярности прямых a и b, будем пользоваться символом 
Теорема 2.1.
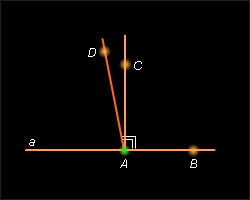
Через каждую точку прямой можно провести перпендикулярную ей прямую и только одну.
Пусть a – данная прямая, а точка A принадлежит прямой. Кроме того, [AB) – один из лучей прямой a. Тогда от луча AB можно отложить угол BAC, равный 90° (аксиома 2.2.). По определению прямая AC  a (рис. 2.3.4).
 4
|
| Рисунок 2.3.4. Перпендикулярные прямые
|
Докажем, что такая прямая AC единственная. Допустим, что существует другая прямая, проходящая через точку A, не совпадающая с прямой AC и перпендикулярная к прямой a. Пусть D – какая-либо точка этой прямой, лежащая в той же полуплоскости от a, что и точка С. Тогда  BAC = BAD = 90°. Но это противоречит аксиоме 2.2, по которой от прямой в данную полуплоскость можно отложить только один угол, равный 90°. Теорема доказана.
|
Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярой данной, имеющий одним из концов их точку пересечения. Этот конец называется основанием перпендикуляра.
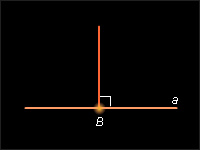 5
|
| Рисунок 2.3.5. Перпендикуляр к прямой
|
Биссектрисой называется луч, проходящий между его сторонами и делящий угол пополам.
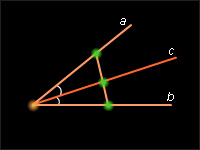 6
|
| Рисунок 2.3.6. Биссектриса
|
