Многоугольник Задачи с решениями
Задачи с решениями

Вычислить сторону правильного пятиугольника, вписанного в окружность радиуса R.
Решение
По теореме 10.4 сторона правильного пятиугольника связана с радиусом описанной окружности формулой 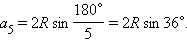 Вычислим величину sin 36°. Рассмотрим для этого равнобедренный треугольник ABC с основанием AC и противолежащим углом 36° (см. рисунок). Проведем биссектрису AD угла A.
Вычислим величину sin 36°. Рассмотрим для этого равнобедренный треугольник ABC с основанием AC и противолежащим углом 36° (см. рисунок). Проведем биссектрису AD угла A.
Так как треугольник ABC равнобедренный, то
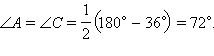 Тогда, поскольку AD – биссектриса, то
Тогда, поскольку AD – биссектриса, то  BAD =
BAD =  DAC = 36°, треугольник ABD равнобедренный, и BD = AD. Кроме того,
DAC = 36°, треугольник ABD равнобедренный, и BD = AD. Кроме того,  ADC – внешний угол треугольника ABD, следовательно,
ADC – внешний угол треугольника ABD, следовательно,  ADC =
ADC =  ABD +
ABD +  BAD = 72°. Тогда треугольник ADC равнобедренный, и AD = AC. Обозначим BD = AD = AC = a. По теореме косинусов в треугольнике ADC имеем DC2 = a2 + a2 – 2a · a · cos 36° = 2a2(1 – cos 36°),
BAD = 72°. Тогда треугольник ADC равнобедренный, и AD = AC. Обозначим BD = AD = AC = a. По теореме косинусов в треугольнике ADC имеем DC2 = a2 + a2 – 2a · a · cos 36° = 2a2(1 – cos 36°),
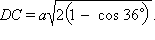 Тогда
Тогда 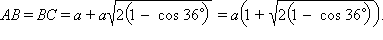 Из свойства биссектрисы имеем (AD – биссектриса):
Из свойства биссектрисы имеем (AD – биссектриса): 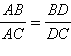 или
или
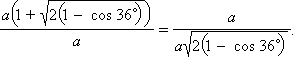 Преобразовав это равенство, получим
Преобразовав это равенство, получим 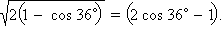 Возведя обе части в квадрат, имеем: 2 – 2 cos 36° = 4 cos2 36° – 4 cos 36° + 1. Обозначим cos 36° = t > 0. Имеем 4t2 – 2t – 1 = 0. Решая уравнение, получим
Возведя обе части в квадрат, имеем: 2 – 2 cos 36° = 4 cos2 36° – 4 cos 36° + 1. Обозначим cos 36° = t > 0. Имеем 4t2 – 2t – 1 = 0. Решая уравнение, получим 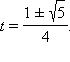 С учетом, что t > 0, получим
С учетом, что t > 0, получим 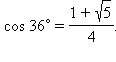 Тогда
Тогда 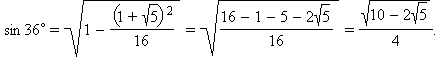 Отсюда
Отсюда 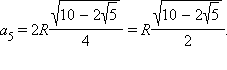
 2 из 5
2 из 5
 |


 Задачи с решениями
Задачи с решениями

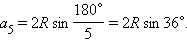 Вычислим величину
Вычислим величину 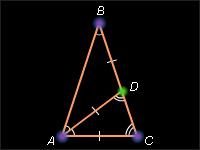
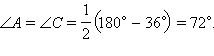 Тогда, поскольку
Тогда, поскольку 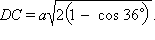 Тогда
Тогда 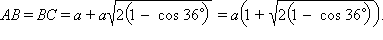 Из свойства биссектрисы имеем
Из свойства биссектрисы имеем 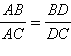 или
или
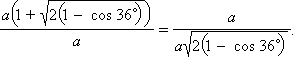 Преобразовав это равенство, получим
Преобразовав это равенство, получим 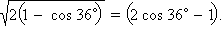 Возведя обе части в квадрат, имеем:
Возведя обе части в квадрат, имеем: 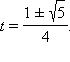 С учетом, что
С учетом, что 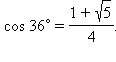 Тогда
Тогда 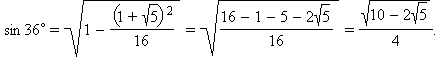 Отсюда
Отсюда 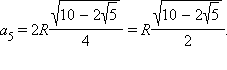
 2 из 5
2 из 5
