

 |
 |
В предыдущих параграфах мы определяли площади частей шара с помощью предельного перехода. Однако такой подход к определению площадей поверхностей в трехмерном пространстве еще не может гарантировать того, что формулы, полученные предельным переходом, дают правильное значение величин этих площадей.
Попытаемся разобраться, чем же многогранные поверхности, построенные в предыдущих примерах, отличаются от исследуемых поверхностей, являющихся частями сферы. Для этого попробуем определить площадь поверхности как предел площади многогранной поверхности и посмотрим, в чем состоит недостаток такого определения.
В одномерном случае длину кривой можно определить так. Отметим на этой кривой несколько точек, которые соединим последовательно. Полученную ломаную можно назвать вписанной в данную кривую. Теперь будем увеличивать число звеньев этой ломаной так, чтобы длина наибольшего звена уменьшалась. Тогда можно определить длину кривой как тот предел, к которому стремится длина ломаной. Поступим аналогично, вписывая в данную поверхность многогранную поверхность и увеличивая число ее граней. Покажем, что площадь многогранной поверхности совсем не обязательно будет стремиться к площади рассматриваемой поверхности. Тем самым станет ясно, что площадь поверхности определяется далеко не так просто, поскольку уже для простейшего тела – цилиндра – мы сейчас получим странный и заведомо неправильный результат.
|
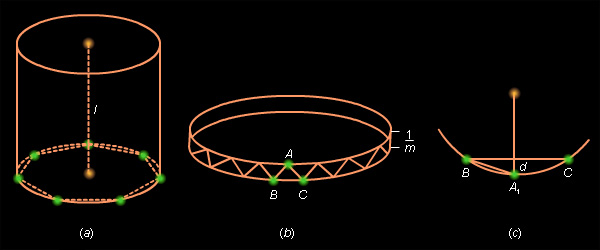
| Рисунок 7.6.1 |
Итак, рассмотрим цилиндр радиуса  Затем вершины каждого многоугольника соединим с ближайшими вершинами соседних многоугольников. В результате получим многогранную поверхность, вписанную в цилиндр, боковая часть которой состоит из треугольников, а верхнее и нижнее основание которой – правильные
Затем вершины каждого многоугольника соединим с ближайшими вершинами соседних многоугольников. В результате получим многогранную поверхность, вписанную в цилиндр, боковая часть которой состоит из треугольников, а верхнее и нижнее основание которой – правильные  Фиксируем теперь число
Фиксируем теперь число  Получается, что высота в каждом треугольнике больше
Получается, что высота в каждом треугольнике больше  Пусть теперь
Пусть теперь  – периметр правильного
– периметр правильного  Значит, площадь части рассматриваемой поверхности, вписанной в боковую поверхность цилиндра, будет больше, чем
Значит, площадь части рассматриваемой поверхности, вписанной в боковую поверхность цилиндра, будет больше, чем  Однако с ростом
Однако с ростом  приближается к длине окружности
приближается к длине окружности
Таким образом, мы убедились, что рассматриваемым способом площадь боковой поверхности круглых тел определить нельзя. Значит, понятие площади боковой поверхности не так просто, как это кажется на первый взгляд. В школьном курсе стереометрии не изучается строгое определение площади боковой поверхности, однако отметим, в чем же дело в рассмотренном примере. Дело в том, что плоскость каждого из треугольников, образующих многогранную поверхность, не приближается к плоскости, касающейся боковой поверхности цилиндра. При строгом же определении понятия площади поверхности круглых тел, таким образом, необходимо требовать кроме приближения многогранной вписанной поверхности к поверхности круглых тел, еще и приближения рассматриваемой поверхности к касательной плоскости данного круглого тела в каждой конкретной точке. В рассматриваемом же примере это было не так. Если мы в одной из вершин треугольника проведем плоскость, касательную к поверхности цилиндра, то угол между этой плоскостью и плоскостью самого треугольника окажется больше некоторой величины.
 |
 |
 |

