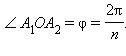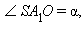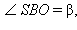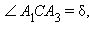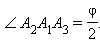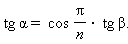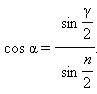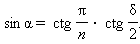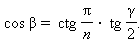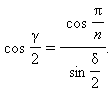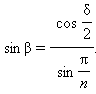Глава 8. Правильные многогранники
8.4. Правильная n-угольная пирамида
Рассмотрим правильную n-угольную пирамиду. Этот многогранник часто встречается в стереометрических задачах, и поэтому более подробное и тщательное изучение его свойств представляет большой интерес. В этом параграфе мы несколько расширим тот арсенал формул, который нами был получен ранее. Запоминать формулы, которые будут выведены в этом параграфе, нет необходимости. Гораздо важнее понять, как они получаются, и научиться применять аналогичные выводы в конкретных задачах.
Итак, пусть SA1A2 … An – правильная n-угольная пирамида (рис. 8.4.1). Введем следующие обозначения:
-
α – угол наклона бокового ребра к плоскости основания;
-
β – двугранный угол при основании;
-
γ – плоский угол при вершине;
-
δ – двугранный угол при боковом ребре.
 1
|
| Рисунок 8.4.1
|
Пусть O – центр основания пирамиды, B – середина ребра 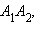 D – точка пересечения отрезков
D – точка пересечения отрезков 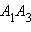 и
и 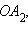 C – точка на боковом ребре
C – точка на боковом ребре 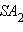 такая, что
такая, что 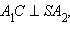 E – точка пересечения отрезков SB и
E – точка пересечения отрезков SB и  K – точка пересечения отрезков
K – точка пересечения отрезков 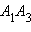 и OB. Пусть
и OB. Пусть 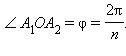
Несложно показать, что 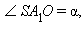
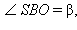
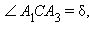
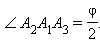
Обозначим также через H высоту пирамиды, апофему – через m, боковое ребро – через l, сторону основания – через a, а через r и R – радиусы окружностей, вписанной в основание и описанной около него.







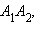
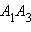 и
и 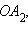
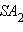 такая, что
такая, что 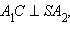

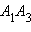 и
и