Глава M. Методика

M.3. Методика работы с компьютерным курсом

M.3.4. Тестовые задания по теме: «Параллельность прямых и плоскостей в пространстве»

Учебные тесты позволяют за сравнительно короткое время получить (и учителю, и ученику) сведения о степени уверенности владения материалом большого раздела курса. Удобства в применении тестов с выбором правильных ответов очевидны: охват сразу большой темы, скорость проверки, возможность оперативной обратной связи с учащимися (ответ неверный – ищите верный; смотрите, где ошибка; повторите материал, к которому относится вопрос); наконец, высокая степень объективности. Недостатки таких тестов не менее очевидны: желательность иметь размноженные тестовые материалы, невозможность получить информацию о "моменте" ошибки ученика, специфичность и некоторое однообразие тестовых вопросов, даже просто затруднения при составлении вопросов, этого можно избежать применяя компьютерные тесты.

Главная направленность тестов – выявить возможные пробелы у каждого ученика, помочь их восполнить. По курсу 10 класса это в основном относится к возможному взаимному расположению прямых и плоскостей (т. е. к пространственному воображению), а также к стандартным вычислительным навыкам. По курсу 11 класса главное внимание обращено на знание основных формул. Тестовые вопросы можно использовать и выборочно, и в текущем учебном процессе, и даже без выбора ответов – просто как задачи.

10 класс. Параллельность в пространстве

1. Сколько существует плоскостей, проходящих через данные прямую и точку в пространстве?

(А) 0	(В) бесконечно много	(Д) 1 или бесконечно много
(Б) 1	(Г) 0 или бесконечно много

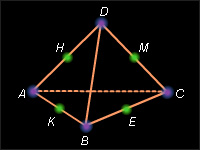
(2–3) Точки K, E, M, H – середины ребер AB, BC, CD, DA тетраэдра ABCD (рис. H.4.1.14.1).

2. Каково взаимное расположение прямых KE и MH?

(А) пересекаются	(В) скрещиваются
(Б) параллельны	(Г) могут быть пересекающимися, параллельными и скрещивающимися (в зависимости от вида тетраэдра)

3. Каково взаимное расположение прямых KM и BC?

(А) пересекаются	(В) скрещиваются
(Б) параллельны	(Г) возможны все три случая (А) – (В)

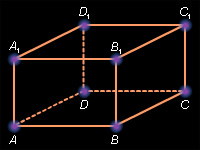
(4–7) Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁ (рис. H.4.1.14.2).

4. Каково взаимное расположение прямых AB₁ и BD₁?

(А) скрещиваются	(В) параллельны	(Д) определить нельзя
(Б) пересекаются	(Г) пересекаются или параллельны

5. Какие из прямых b = BB₁, c = CC₁, d = D₁C₁ скрещиваются с прямой a = AB?

(А) только b	(В) только c и d	(Д) все три прямые b, c, d
(Б) только c	(Г) только b и c

1

Рисунок M.3.4.1

2

Рисунок M.3.4.2

6. Каково взаимное расположение прямой B₁C₁ и плоскости BDA₁?

(А) параллельны	(В) пересекаются или параллельны
(Б) пересекаются	(Г) ответ отличен от (А) – (В)

7. Каково взаимное расположение плоскостей BDA₁ и B₁D₁C?

(А) параллельны	(В) пересекаются или параллельны
(Б) пересекаются	(Г) ответ отличен от (А) – (В)

8. В пространстве даны прямая a и точка M. Сколько существует прямых, проходящих через M и параллельных прямой a?

(А) 0	(В) бесконечно много	(Д) 1 или бесконечно много
(Б) 1	(Г) 0 или 1

9. Даны плоскость и точка M вне плоскости. Сколько существует прямых, проходящих через M и параллельных плоскости?

(А) 0	(В) бесконечно много	(Д) 1 или бесконечно много
(Б) 1	(Г) 0 или бесконечно много

10. Даны параллельные прямая a и плоскость α. Сколько существует плоскостей, проходящих через a и параллельных α?

(А) 0	(В) бесконечно много	(Д) бесконечно много
(Б) 1	(Г) 0 или 1

11. В пространстве даны две параллельные прямые a и b. Сколько существует плоскостей, проходящих через прямую a и параллельных прямой b?

(А) 0	(В) бесконечно много	(Д) 1 или бесконечно много
(Б) 1	(Г) 0 или 1

12. Даны две пересекающиеся плоскости α, β и не лежащая на них точка M. Сколько существует прямых, проходящих через M и параллельных плоскостям α и β?

(А) 0	(В) бесконечно много	(Д) 0 или бесконечно много
(Б) 1	(Г) 0 или 1

13. Даны две скрещивающиеся прямые a и b. Сколько существует пар параллельных плоскостей, одна из которых проходит через a, а другая – через b?

(А) 0	(В) бесконечно много	(Д) 0 или бесконечно много
(Б) 1	(Г) 0 или 1

14. В пространстве даны две пересекающиеся прямые a, b и не лежащая на них точка M. Сколько существует плоскостей, проходящих через M и параллельных прямым a и b?

(А) 0	(В) бесконечно много	(Д) 0 или бесконечно много
(Б) 1	(Г) 0 или 1

15. Точки A, B и середина M отрезка AB проектируются в точки A₁, B₁ и M₁. Чему равна длина отрезка MM₁, если AA₁ = 3 см, B₁B = 7 см?

(А) 5 см	(В) 2 см	(Д) ответ отличен от указанных
(Б) 4 см	(Г) 5 см или 2 см

16. В пространстве даны прямая a и точка M. Сколько существует плоскостей, проходящих через M и перпендикулярных прямой a?

(А) 0	(В) бесконечно много	(Д) 1 или бесконечно много
(Б) 1	(Г) 0 или 1

17. Даны плоскость α и не лежащая в ней прямая a. Сколько существует плоскостей, проходящих через прямую a и перпендикулярных плоскости α?

(А) 0	(В) бесконечно много	(Д) 1 или бесконечно много
(Б) 1	(Г) 0 или 1

18. Даны три параллельные плоскости α, β, γ. Расстояние между α и β равно 3, расстояние между β и γ равно 5. Чему равно расстояние между плоскостями α и γ?

(А) 2	(В) 8	(Д) 4 или 8
(Б) 4	(Г) 2 или 8

19. В пространстве даны три параллельные прямые a, b, c. Расстояние между a и b равно 2, расстояние между b и c равно 6. Чему равно расстояние x между прямыми a и c?

(А) 0 < x < 6	(В) 2 < x < 8	(Д) 4 < x < 6
(Б) 0 < x < 8	(Г) 4 < x < 8

20. Известно, что прямая a параллельна прямой b, а прямая b пересекается с плоскостью γ. Каково взаимное расположение прямой a и плоскости γ?

(А) обязательно пересекаются	(В) пересекаются или параллельны (т. е. могут и пересекаться, и быть параллельными)
(Б) обязательно параллельны	(Г) ответ отличен от (А) – (В)

21. Известно, что прямая a параллельна прямой b, а прямая b параллельна прямой c. Каково взаимное расположение прямых a и c?

(А) обязательно параллельны	(В) параллельны или скрещиваются	(Д) параллельны или совпадают
(Б) обязательно скрещиваются	(Г) параллельны, скрещиваются или пересекаются

22. Известно, что прямая a параллельна прямой b, а прямая b параллельна плоскости γ. Каково взаимное расположение прямой a и плоскости γ?

(А) обязательно параллельны	(В) параллельны или пересекаются
(Б) обязательно пересекаются	(Г) ответ отличен от (А) – (В)

23. Известно, что плоскость α параллельна прямой β, а прямая β параллельна плоскости γ, отличной от α. Каково взаимное расположение плоскостей α и γ?

(А) обязательно параллельны	(В) параллельны или пересекаются
(Б) обязательно пересекаются	(Г) ответ отличен от (А) – (В)

24. Даны три различные прямые a, b и c. Известно, что a скрещивается с b, a b скрещивается с прямой c. Каково взаимное расположение прямых a и c?

(А) обязательно скрещиваются	(В) скрещиваются, пересекаются или параллельны	(Д) ответ отличен от указанных
(Б) скрещиваются или пересекаются	(Г) скрещиваются или параллельны

25. Даны две скрещивающиеся прямые a, b и не лежащая на них точка M. Сколько существует плоскостей, проходящих через M и параллельных прямым a и b?

(А) 0	(В) 0 или 1	(Д) О, 1 или бесконечно много
(Б) 1	(Г) 0 или 1,2

26. Даны две скрещивающиеся прямые a и b. Сколько существует плоскостей, проходящих через прямую a и перпендикулярных прямой b?

(А) 0	(В) бесконечно много	(Д) 0 или бесконечно много
(Б) 1	(Г) 0 или 1

27. Даны три попарно скрещивающиеся прямые a, b и c. Сколько существует прямых, пересекающих все эти три прямые?

(А) 0	(В) бесконечно много	(Д) 1 илиcбесконечно много
(Б) 1	(Г) 0 или бесконечно много

28. На ребрах AD, AB и CD тетраэдра ABCD произвольно взяты точки K, E, M. Какие ребра, кроме трех указанных, пересекает плоскость KEM?

(А) AC	(В) BD	(Д) определить нельзя
(Б) BC	(Г) никакие

29. Какие из следующих фигур можно получить как параллельную проекцию куба:
I – ромб (не квадрат), II – правильный 5-угольник, III – правильный 6-угольник?

(А) только фигуру I	(В) фигуры II и III	(Д) все три фигуры
(Б) фигуры I и II	(Г) фигуры I и III