|
|
|
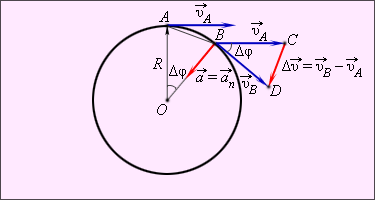
Рис. 1. Центростремительное ускорение тела 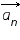
при равномерном движении по окружности |
При равномерном движении по окружности скорость точки (тела) меняется по направлению, но не меняется по величине. Рассмотрев треугольники на рис. 1, можно доказать, что:
- ускорение при равномерном движении по окружности направлено к центру окружности (поэтому оно называется центростремительным);
- величина этого центростремительного ускорения может быть вычислена по формуле
Характерные величины центростремительных ускорений в космических масштабах:
- Земля при вращении вокруг оси: aцс = 0,03 м/с2,
- Земля при обращении вокруг Солнца: aцс = 0,006 м/с2,
- Солнечная система при обращении вокруг центра Галактики: aцс = 3∙10—10 м/с2.
|
|
|
Рис. 2. Направление ускорения при равномерном движении по окружности
|
|
|
|
|
Центростремительное ускорение меняет скорость только по направлению, но не меняет по величине. Вектор центростремительного ускорения перпендикулярен вектору скорости.
|
|
|
|
|
|
В том случае, если скорость тела при движении по окружности меняется по величине, то появляется еще одно ускорение, направленное по касательной к окружности (параллельно вектору скорости).
Направление вектора полного ускорения 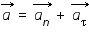 определяется в каждой точке круговой траектории величинами нормального и касательного ускорений по правилу треугольника.
определяется в каждой точке круговой траектории величинами нормального и касательного ускорений по правилу треугольника.
|
|
Рис. 3. Составляющие ускорения 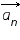
и 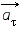
при неравномерном движении тела по окружности |
|
|




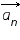 при равномерном движении по окружности
при равномерном движении по окружности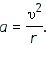




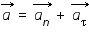 определяется в каждой точке круговой траектории величинами нормального и касательного ускорений по правилу треугольника.
определяется в каждой точке круговой траектории величинами нормального и касательного ускорений по правилу треугольника.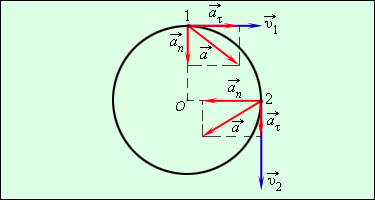
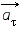 при неравномерном движении тела по окружности
при неравномерном движении тела по окружности