|
Если сила действует на тело, движущееся по оси x и перемещающееся на 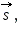 то можно ввести характеристику — работу.
то можно ввести характеристику — работу.
|
|
|
Рис. 1. Механическая работа
|
|
|
|
|
Работа — физическая величина, характеризующая результат действия силы и численно равная скалярному произведению вектора силы и вектора перемещения, совершенного под действием этой силы
|
|
|
|
|
|
|
|
Рис. 2. Работа силы 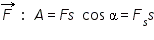 |
Работа не совершается, если:
- Сила действует, а тело не перемещается.
Например, мы действуем с силой на шкаф, но не можем сдвинуть.
- Тело перемещается, а сила равна нулю или все силы скомпенсированы.
Например: при движении по инерции работа не совершается.
- Угол между векторами силы и перемещения (мгновенной скорости) равен 90° (cos α = 0).
Например: центростремительная сила работу не совершает.
Если вектора силы и перемещения сонаправлены (α = 0°, cos 0 = 1), то A = Fs.
Если вектора силы и перемещения направлены противоположно (α = 180°, cos 180° = —1), то A = —Fs (например, работа силы сопротивления, трения).
Если угол между векторами силы и перемещения 0° < α < 90°, то работа положительна.
Если угол между векторами силы и перемещения 90° < α < 180°, то работа отрицательна.
|
|
|
|
Если на тело действует несколько сил, то полная работа (работа всех сил) равна работе результирующей силы.
|
|
|
|
|
|
Если сила меняется с расстоянием (координатой), то необходимо разбить все движение на такие малые участки, на которых силу можно считать неизменной, сосчитать работы на каждом элементарном участке пути, и сложить все элементарные работы.
|
|




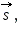 то можно ввести характеристику — работу.
то можно ввести характеристику — работу.