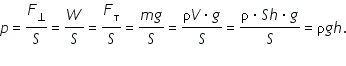Внутри жидкости в любой ее точке существует давление, обусловленное тем, что верхние слои из-за притяжения к земле своим весом действуют на нижние слои. Гидростатическое или весовое давление — это давление, создаваемое весом покоящейся жидкости.

Простые наблюдения позволяют сделать вывод, что давление, создаваемое жидкостью на дно сосуда, зависит от высоты столба жидкости и от рода жидкости.

Рис. 1. Зависимость растяжения резиновой пленки от высоты столба и рода жидкости

В 1648 году зависимость давления жидкости от высоты ее столба продемонстрировал Блез Паскаль. Он вставил в закрытую бочку, наполненную водой, трубку диаметром 1 см², длиной 5 м и, поднявшись на балкон второго этажа дома, вылил в эту трубку большую кружку воды. Когда вода в ней поднялась до высоты 4 метра, давление воды увеличилось настолько, что в крепкой дубовой бочке образовались щели, через которые наружу потекла вода.

Рис. 2. Опыт Паскаля

Получим формулу для гидростатического давления.

Сила F, с которой жидкость давит на дно сосуда, является весом жидкости. Его мы можем подсчитать по формуле W = F_т = mg, так как жидкость и ее опора (дно сосуда) покоятся. Вспомним также формулу m = ρV для выражения массы тела через плотность его вещества и формулу V = Sh для подсчета объема тела, площадью S и высотой h. В результате имеем равенство:

Здесь:

p — давление слоя жидкости, Па;

ρ — плотность жидкости, кг/м³;

h — высота слоя жидкости, м;

g = 9,8 м/с² — ускорение свободного падения.

Заметим также, что формула будет справедлива и для газа, заключенного в соответствующий сосуд.

Формула p = ρgh показывает, что давление, создаваемое слоем жидкости, не зависит от ее массы, а зависит от плотности жидкости, высоты ее слоя и места наблюдения.

На рис. 1 продемонстрирован гидростатический парадокс. Давление и сила давления на дно всех трех сосудов равны (при равенстве высоты столбов жидкости и площади дна).

Вес жидкости, налитой в сосуд, может отличаться от силы давления, оказываемой ею на дно сосуда. Так, в расширяющихся кверху сосудах сила давления на дно меньше веса жидкости, а в суживающихся — больше. В цилиндрическом сосуде обе силы одинаковы. Объясняется гидростатический парадокс тем, что, поскольку гидростатическое давление p всегда нормально к стенкам сосуда, сила давления на наклонные стенки имеет вертикальную составляющую p₁, которая компенсирует вес излишнего против левого цилиндра объема жидкости в правом сосуде и вес недостающего объема жидкости в сосуде, расположенном по центру. Гидростатический парадокс обнаружен Блезом Паскалем (1654).

При увеличении толщины слоя жидкости или ее плотности гидростатическое давление будет возрастать. Гидростатическое давление на морских глубинах очень велико, поэтому человек не может находиться на глубине без специальных аппаратов.

Искатели жемчуга погружаются до глубин в 30 м, рекордное погружение человека без специального оснащения составляет 105 м. С аквалангом человек может опуститься на глубину до 100—140 метров. Защитив себя корпусом подводной лодки, человек может опуститься уже до километра вглубь моря. И лишь специальные аппараты — батискафы и батисферы — позволяют опускаться до глубин в несколько километров.

При быстром изменении давления окружающей среды у человека возникает кессонная болезнь. При работе в условиях повышенного давления ткани человека поглощают дополнительное количество азота. При чрезмерно быстром переходе из среды с более высоким давлением в среду с более низким давлением растворённый в тканях избыточный азот освобождается, образуя пузырьки газа. Эти пузырьки закупоривают кровеносные сосуды, мешая движению крови, и человек может погибнуть. Поэтому аквалангисты всплывают медленно, чтобы кровь успевала уносить образующиеся пузырьки газа в легкие.

Рис. 4. Аквалангисты