|
Скорость и ускорение при гармонических колебаниях |  |
 |

|
При гармонических колебаниях координаты тела, его скорость и ускорение также меняются гармонически. Если
и ускорения
Амплитуда скорости равна υm = ω0 Ускорение при гармонических колебаниях также изменяется гармонически. Амплитуда ускорения
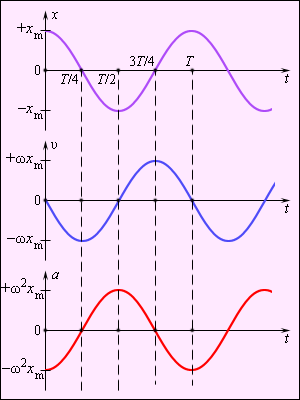
Ускорение и смещение одновременно становятся максимальными по модулю, но имеют противоположные знаки. В таких случаях говорят, что колебания смещения и ускорения происходят в противофазе. На рис. 1 приведены графики координаты, скорости и ускорения тела, совершающего гармонические колебания.
|
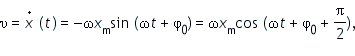
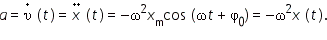
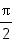 . В момент, когда координата равна нулю (момент прохождения равновесия), модуль скорости максимален. Скорость равна нулю, когда смещение максимально по модулю.
. В момент, когда координата равна нулю (момент прохождения равновесия), модуль скорости максимален. Скорость равна нулю, когда смещение максимально по модулю.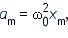 а по фазе колебания ускорения опережают колебания координаты на π.
а по фазе колебания ускорения опережают колебания координаты на π.