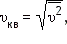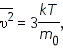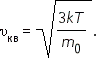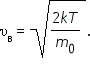|
Движение молекул в идеальном газе |  |
 |

|
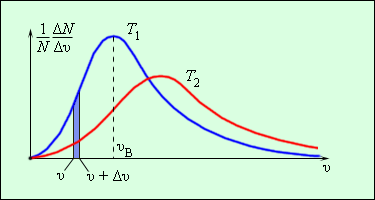
Молекулы газа вследствие теплового движения испытывают многочисленные соударения друг с другом. При каждом соударении скорости молекул изменяются как по величине, так и по направлению. В результате в сосуде, содержащем большое число молекул, устанавливается некоторое статистическое распределение молекул по скоростям, зависящее от абсолютной температуры Джеймс Максвелл в 1860 году вывел закон распределения молекул газа по скоростям, исходя из основных положений молекулярно-кинетической теории. На рис. 1 представлены типичные кривые распределения молекул по скоростям. По оси абсцисс отложен модуль скорости, а по оси ординат — относительное число молекул, скорости которых лежат в интервале от υ до υ + Δυ. Это число равно площади выделенного на рис. 1 столбика.
Характерными параметрами распределения Максвелла являются наиболее вероятная скорость υв, соответствующая максимуму кривой распределения, и среднеквадратичная скорость
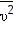 — среднее значение квадрата скорости. — среднее значение квадрата скорости.
Средний квадрат скорости
где Квадратный корень из этой величины называется средней квадратичный скоростью:
С ростом температуры максимум кривой распределения смещается в сторону больших скоростей, при этом υв и υкв увеличиваются. Согласно распределению Максвелла оказывается, что:
При любой температуре газа имеется некоторое количество молекул, скорости которых, а значит, и кинетические энергии, заметно превышают средние. «Быстрые» молекулы объясняют протекание ряда химических реакций (горение топлива) и некоторые физические явления. Например, испарение воды при комнатной температуре происходит за счет небольшого числа быстрых молекул. |