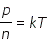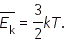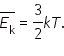Таким образом, физическая величина выравнивается при тепловом равновесии, то есть ведет себя как температура. Эту новую температуру назовем энергетической температурой, учитывая, что в системе СИ она измеряется в джоулях.

При абсолютном нуле температур давление, и, следовательно, отношение равно нулю. Отсюда следует, что энергетическая шкала температур является абсолютной.

Любые две абсолютные шкалы температур можно связать коэффициентом пропорциональности. Для энергетической шкалы и шкалы Кельвина получаем:

или

где k — коэффициент пропорциональности, некоторая универсальная постоянная величина. Ее называют постоянной Больцмана.

Сравнивая соотношения p = nkT с основным уравнением молекулярно-кинетической теории газов, можно получить

Средняя кинетическая энергия хаотического движения молекул газа прямо пропорциональна абсолютной температуре.

Это уравнение прокладывает мостик между двумя мирами, связывая характеристики атомного уровня (в левой части) с макроскопическими величинами (в правой части), которые можно измерить при помощи приборов, в данном случае термометров.

Таким образом, температура есть мера средней кинетической энергии поступательного движения молекул. Постоянная Больцмана связывает температуру со средней кинетической энергией движения молекул в веществе. Температура прямо пропорциональна средней кинетической энергии теплового движения частиц вещества. Следовательно, температуру можно назвать мерой средней кинетической энергии частиц, характеризующей интенсивность теплового движения молекул. Этот вывод хорошо согласуется с экспериментальными данными, показывающими увеличение скорости частиц вещества с ростом температуры. Рассуждения, которые мы проводили для выяснения физической сущности температуры, относятся к идеальному газу. Однако выводы, полученные нами, справедливы не только для идеального, но и для реальных газов. Справедливы они и для жидкостей и твердых тел. В любом состоянии температура вещества характеризует интенсивность теплового движения его частиц.