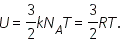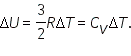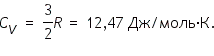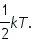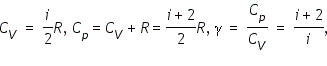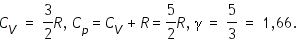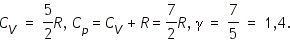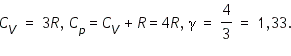|
Теорема о равномерном распределении энергии по степеням свободы |  |
 |

|
В молекулярно-кинетической теории устанавливается следующее соотношение между средней кинетической энергией
Внутренняя энергия 1 моля идеального газа равна произведению
При изменении температуры на Δ
Коэффициент пропорциональности между Δ
Это соотношение хорошо подтверждается в экспериментах с газами, состоящими из одноатомных молекул (гелий, неон, аргон). Однако, для двухатомных (водород, азот) и многоатомных (углекислый газ) газов это соотношение не согласуется с экспериментальными данными. Причина такого расхождения состоит в том, что для двух- и многоатомных молекул средняя кинетическая энергия должна включать не только энергию поступательного движения, но и энергию вращательного движения молекул.
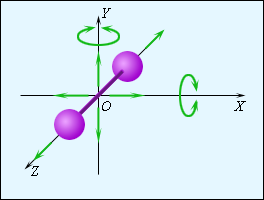
На рис. 1 изображена модель двухатомной молекулы. Молекула может совершать пять независимых движений: три поступательных движения вдоль осей В классической статистической физике доказывается так называемая теорема о равномерном распределении энергии по степеням свободы:
Из этой теоремы следует, что молярные теплоемкости газа
где Для газа, состоящего из одноатомных молекул (
Для газа, состоящего из двухатомных молекул (
Для газа, состоящего из многоатомных молекул (
Экспериментально измеренные теплоемкости многих газов при обычных условиях достаточно хорошо согласуются с приведенными выражениями. Однако, в целом классическая теория теплоемкости газов не может считаться вполне удовлетворительной. Существует много примеров значительных расхождений между теорией и экспериментом. Это объясняется тем, что классическая теория не в состоянии полностью учесть энергию, связанную с внутренними движениями в молекуле. |
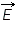 поступательного движения молекул и абсолютной температурой
поступательного движения молекул и абсолютной температурой 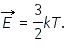
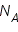 :
: