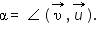|
Пусть имеются две системы отсчета. Система XOY условно считается неподвижной, а система X'O'Y' движется поступательно по отношению к системе XOY со скоростью 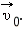 Система XOY может быть, например, связана с Землей, а система X'O'Y' — с движущейся по рельсам платформой.
Система XOY может быть, например, связана с Землей, а система X'O'Y' — с движущейся по рельсам платформой.
|
|
|
Рис. 1. Преобразования Галилея
|
Пусть человек перешел по платформе за некоторое время из точки A в точку B. Тогда его перемещение относительно платформы соответствует вектору 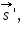 а перемещение платформы относительно земли соответствует вектору а перемещение платформы относительно земли соответствует вектору 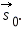 Из рис. 1 видно, что перемещение человека относительно земли будет соответствовать вектору Из рис. 1 видно, что перемещение человека относительно земли будет соответствовать вектору 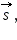 представляющему собой сумму векторов представляющему собой сумму векторов 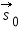 и
и 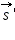 . .
Это уравнение представляет собой правило сложения перемещений.
|
|
|
Модель 1. Сложение и вычитание векторов
|
Если правую и левую часть разделить на время движения t, получим:
Это уравнение представляет собой закон сложения скоростей.
В общем случае, для движений, происходящих под любым углом друг к другу:
|
|
|
|
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости точки относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной.
|
|
|
|
|
|
Для прямолинейного движения закон сложения скоростей можно записать в проекциях:
Скорость подвижной системы отсчета относительно неподвижной называется переносной скоростью.
При решении задач часто бывает удобно принимать одно из движущихся относительно земли тел за неподвижное. Тогда скорость земли в этой системе отстчета будет равна по величине и противоположна по направлению скорости данного тела.
Если скорости υ1 и u сонаправлены (тела сближаются), то их проекции складываются, если противоположно направлены (тела удаляются) — вычитаются.
Если скорости υ1 и u направлены под прямым углом, то 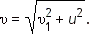 Если же угол произвольный, то необходимо пользоваться теоремой косинусов:
Если же угол произвольный, то необходимо пользоваться теоремой косинусов: 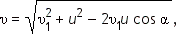 где где 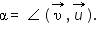
Эти выводы справедливы для скоростей, много меньших скорости света в вакууме (3∙108 м/с).
|




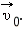 Система
Система 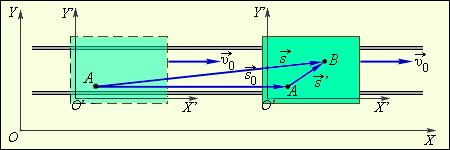
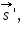 а перемещение платформы относительно земли соответствует вектору
а перемещение платформы относительно земли соответствует вектору 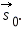 Из рис. 1 видно, что перемещение человека относительно земли будет соответствовать вектору
Из рис. 1 видно, что перемещение человека относительно земли будет соответствовать вектору 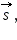 представляющему собой сумму векторов
представляющему собой сумму векторов 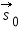 и
и 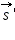 .
.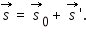




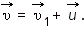
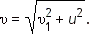 Если же угол произвольный, то необходимо пользоваться теоремой косинусов:
Если же угол произвольный, то необходимо пользоваться теоремой косинусов: 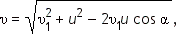 где
где