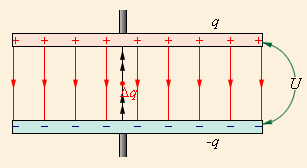
Заряженный конденсатор, как и любая другая система заряженных тел, обладает энергией. В этом можно убедиться, если к пластинам заряженного конденсатора большой емкости подключить лампочку карманного фонарика. На короткое время лампочка вспыхнет.

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо совершить, чтобы зарядить конденсатор, то есть разделить положительные и отрицательные заряды.

Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq > 0 с одной обкладки на другую. При этом одна обкладка постепенно заряжается положительным зарядом, а другая — отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд q, а между ними существует некоторая разность потенциалов U = q/C, то при переносе каждой порции Δq внешние силы должны совершить работу

.

Энергия W_e конденсатора емкости C, заряженного зарядом Q, может быть найдена путем интегрирования этого выражения в пределах от 0 до Q:

Рис. 1. Процесс зарядки конденсатора

Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением Q = CU.

.

Полученные формулы справедливы для энергии любого конденсатора, а не только плоского.

По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля.
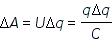
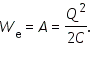
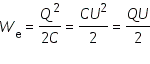