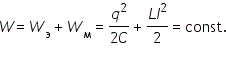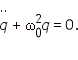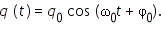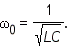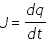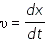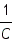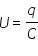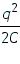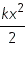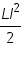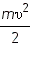В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является колебательный контур — цепь, состоящая из последовательно включенных катушки c индуктивностью L и конденсатора c емкостью C.

Рис. 1. Колебательный контур

Если зарядить конденсатор и замкнуть ключ, то начинается процесс разрядки конденсатора через катушку индуктивности L. Согласно закону электромагнитной индукции, ток в катушке нарастает постепенно и принимает максимальное значение, когда конденсатор разрядится. Затем ток начинает постепенно убывать, перезаряжая при этом конденсатор. При свободных колебаниях (R = 0) происходит периодическое превращение электрической энергии W_э, запасенной в конденсаторе, в магнитную энергию W_м катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:

Продифференцировав это уравнение и учитывая, что электрический ток есть первая производная от заряда, получим уравнение гармонических колебаний:

Таким образом, в отсутствие затухания колебания заряда в электрическом контуре являются гармоническими, то есть происходят по закону:

Параметры L и C колебательного контура определяют собственную частоту и период свободных колебаний в колебательном контуре (формула Томсона):

Амплитуда q₀ и начальная фаза φ₀ определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия.

Можно провести полную аналогию процессов свободных электрических и механических колебаний. На рисунке приведены графики изменения заряда q (t) конденсатора и смещения x (t) груза от положения равновесия, а также графики тока J (t) и скорости груза υ (t) за один период колебаний.

Сравнение свободных колебаний груза на пружине и процессов в электрическом колебательном контуре позволяет сделать заключение об аналогии между электрическими и механическими величинами. Эти аналогии представлены в таблице:

Электрические величины Механические величины Заряд конденсатора q (t) Координата x (t) Ток в цепи 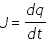Скорость 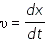Индуктивность L Масса m Величина, обратная электроемкости 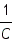Жесткость k Напряжение на конденсаторе 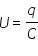Упругая сила kx Энергия электрического поля конденсатора 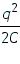Потенциальная энергия пружины 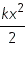Магнитная энергия катушки 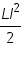Кинетическая энергия 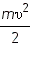Магнитный поток LI Импульс mυ

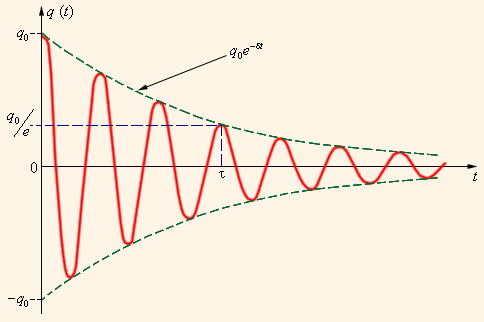
Все реальные контуры содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими.

Рис. 2. Затухающие колебания в контуре

Колебательный контур нашел широкое применение в радиосвязи для настройки частоты приемной антенны в резонанс с той или иной частотой передающей антенны.

Рис. 3. Принципы радиосвязи