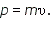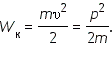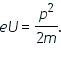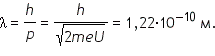|
Гипотеза де Бройля о волновых свойствах частиц |  |
 |

|
Законы фотоэффекта свидетельствуют, что свет при испускании и поглощении ведет себя подобно потоку частиц, получивших название фотонов или световых квантов. Энергия фотонов равна:
Фотон движется в вакууме со скоростью
Таким образом, учение о свете, совершив виток длительностью в два столетия, вновь возвратилось к представлениям о световых частицах — корпускулах. Но это не был механический возврат к корпускулярной теории Ньютона. В начале XX века стало ясно, что свет обладает двойственной природой. При распространении света проявляются его волновые свойства (интерференция, дифракция, поляризация), а при взаимодействии с веществом — корпускулярные (фотоэффект). Эта двойственная природа света получила название корпускулярно-волнового дуализма. Позже двойственная природа была открыта у электронов и других элементарных частиц. Классическая физика не может дать наглядной модели сочетания волновых и корпускулярных свойств у микрообъектов. Движением микрообъектов управляют не законы классической механики Ньютона, а законы квантовой механики. Единство корпускулярных и волновых свойств микрообъектов — одна из ведущих идей квантовой теории. В 1923 году произошло примечательное событие, которое в значительной степени ускорило развитие квантовой физики. Французский физик Луи де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны, и любые другие частицы материи наряду с корпускулярными обладают также и волновыми свойствами. Согласно де Бройлю, с каждым микрообъектом связаны, с одной стороны, корпускулярные характеристики — энергия Корпускулярные и волновые характеристики микрообъектов связаны такими же количественными соотношениями, как и у фотона:
Гипотеза де Бройля распространила эти соотношения для всех микрочастиц, в том числе и для таких, которые обладают массой
Гипотеза де Бройля основывалась на соображениях симметрии свойств материи и не имела в то время опытного подтверждения.
Можно ли наблюдать волновые свойства у макроскопических тел? Волновые свойства (интерференция и дифракция) у макроскопических тел можно наблюдать с воображаемым экспериментальным устройством, создающим разность хода Δ порядка длины волны λ. Определим длину волны де Бройля для макроскопического тела массой 1 г, движущегося со скоростью υ = 1 м/с. Импульс тела Пылинке массой 10—9 г, движущейся со скоростью 0,5 м/с, соответствует волна де Бройля с длиной волны порядка 10—21 м, т. е. приблизительно на 11 порядков меньше размеров атома. Вследствие большой массы макроскопических тел их волновые свойства не могут быть обнаружены экспериментально. Такая длина волны лежит за пределами доступной наблюдению области. Этот пример показывает, что макроскопические тела могут проявлять только корпускулярные свойства. Определим длину волны де Бройля для электрона. Кинетическая энергия электрона, движущегося с небольшими скоростями, может быть выражена через импульс
Затем работу электрического поля
Пусть электрон ускоряется разностью потенциалов 100 В. Длина волны де Бройля Полученная величина имеет порядок межатомных расстояний в кристалле. Значит, отражение «электронных волн» от параллельных слоев атомов в кристалле можно использовать для обнаружения волновых свойств электронов. |
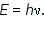
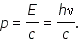
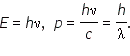
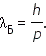
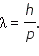
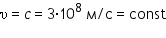
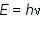
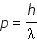
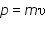
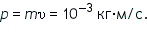 Длина волны де Бройля
Длина волны де Бройля 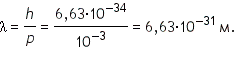 Таким образом, для макроскопических тел длина волны де Бройля чрезвычайно мала, в
Таким образом, для макроскопических тел длина волны де Бройля чрезвычайно мала, в 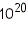 меньше размеров атомов, в
меньше размеров атомов, в 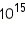 меньше размеров ядер атомов.
меньше размеров ядер атомов.