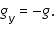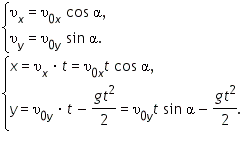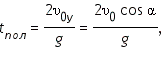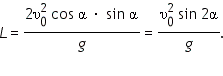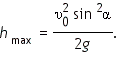|
Свободное падение тел происходит под прямым углом к горизонту. Движение тела может происходить под действием силы тяжести, брошенного горизонтально или под любым углом к горизонту.
|
|
|
|
- Это движение в плоскости, поэтому для описания движения необходимо 2 координаты.
- Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела — ускорение свободного падения (a = g).
- Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) — вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное.
|
|
|
|
|
|
|
|
|
Рис. 1. Движение тела, брошенного горизонтально
|
Выразим проекции скорости и координаты через модули векторов.
Для того чтобы получить уравнение траектории, выразим время t из уравнения координаты x и подставим в уравнение для y: 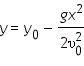 — между координатами квадратичная зависимость, траектория — парабола!
— между координатами квадратичная зависимость, траектория — парабола!
|
|
|
Рис. 2. Движение тела, брошенного под углом к горизонту
|
Начальные условия: x0 = 0 и y0 = 0. Проекция ускорения свободного падения на ось у отрицательна и равна модулю ускорения свободного падения:
Решение этой системы уравнений приводит к выводу — тело движется по параболе.
|
|
|
|
При этом время полета тела от начальной точки до точки падения будет равно:
а расстояние, которое пролетит тело:
|
|
|
|
|
|
Из этой формулы следует, что:
|
|
|
|
- Максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 45°.
- На одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами — так называемые навесная и настильная баллистические траектории.
|
|
|
|
|
|
Настильными траекториями называют траектории, получаемые при углах, меньших угла наибольшей дальности, траектории 1 и 2. Навесными траекториями называют траектории, получаемые при углах, больших угла наибольшей дальности, например, траектории 3 и 4.
|
|
|
Модель 1. Навесная и настильная траектории полета
|
|
|
|
|
- Максимальная высота, которой может достичь тело:
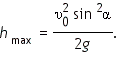
- Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе).
|
|
|
|
|
|
|
|








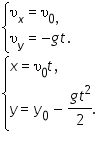
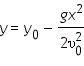 — между координатами квадратичная зависимость, траектория — парабола!
— между координатами квадратичная зависимость, траектория — парабола!