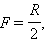Глава 2. Свет и вещество

2.1. Природа света

2.1.2. Законы геометрической оптики

Геометрическая оптика рассматривает излучение как тонкие пучки света – лучи, в однородной среде распространяющиеся прямолинейно. Геометрическая оптика базируется на четырех аксиомах.

1

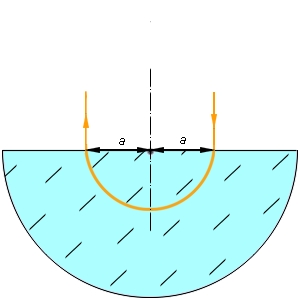
Рисунок 2.1.2.1. Геометрическая оптика допускает искривление лучей света в оптически неоднородных средах. На приведенном рисунке показатель преломления вещества в полусфере зависит от расстояния до ее центра по формуле n = n0 / (1 + (r/r0)2). Луч, падающий нормально на расстоянии r0 от центра полусферы, выйдет с другой стороны полусферы на том же расстоянии от центра

1. Лучи света распространяются независимо друг от друга. Суммарная интенсивность двух пучков равна сумме интенсивностей каждого пучка в отсутствие другого (принцип суперпозиции). Нарушение этой аксиомы сопровождается интерференцией, изучение которой выходит за рамки геометрической оптики.
2. В однородной среде лучи света распространяются прямолинейно. В начале XIX века было открыто явление огибания светом препятствий, получившее название дифракции.
3. Закон отражения света: угол падения светового луча равен углу его отражения. Падающий и отраженный лучи, а также перпендикуляр, восстановленный в точке падения, лежат в одной плоскости.
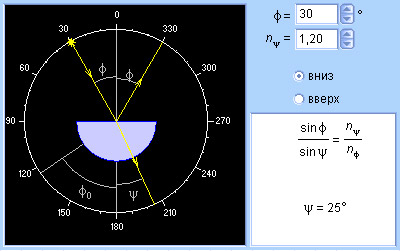
4. Закон Снеллиуса: отношение синуса угла падения к синусу угла преломления есть величина, постоянная для двух сред:

   Падающий и преломленный лучи, а также перпендикуляр, восстановленный в точке падения, лежат в одной плоскости.

Модель 2.1. Законы геометрической оптики

Для упрощения расчетов в геометрической оптике часто используется приближение параксиального пучка лучей. Суть его в том, что рассматриваются только лучи, распространяющиеся вблизи оптической оси системы и образующие очень малые углы с этой осью и нормалями к отражающим и преломляющим поверхностям системы. Когда угол между оптической осью и падающим лучом мал, можно считать, что sin φ ≈ tg φ ≈ φ. Отклонения от законов параксиальной оптики в оптических приборах приводят к появлению различных аберраций.

2

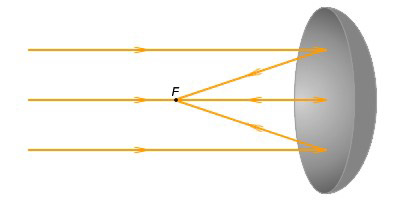
Рисунок 2.1.2.2. Пучок параллельных лучей в приближении параксиальной оптики собирается в фокусе сферического зеркала

Пучок параллельных лучей, распространяющийся вдоль оптической оси, в приближении параксиальной оптики после отражения от сферического зеркала соберется в одной точке, называемой фокусом сферического зеркала. Эта точка отстоит от центра сферы на расстояние 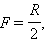где R – радиус сферы. Связь между расстоянием до предмета (f) и расстоянием до изображения (d) дается формулой:

3

Рисунок 2.1.2.3. При прохождении через положительную (выпуклую) линзу пучок параллельных лучей собирается в одной точке

Параллельные пучки собирает в точку не только зеркало, но и выпуклая линза. Если расстояние до фокуса линзы равно F, то формула линзы записывается следующим образом:

4

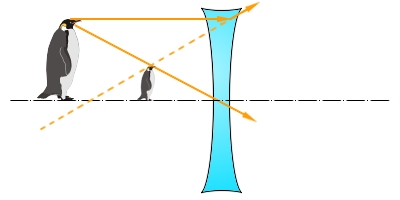
Рисунок 2.1.2.4. Рассеивающая (вогнутая) линза дает прямое мнимое изображение предмета

Если изображение источника стало мнимым и находится с той же стороны от линзы, что и источник, то предыдущая формула примет вид:

5

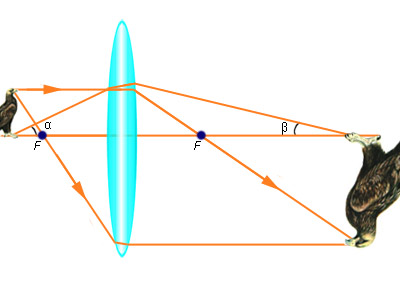
Рисунок 2.1.2.5. Угловое увеличение линзы

Наконец, в случае вогнутой линзы перед фокусным расстоянием появляется минус.

Линейным увеличением оптической системы называется отношение величины изображения предмета к величине самого предмета. В астрономии чаще применяют понятие угловое увеличение:

Отражение света от гладких полированных поверхностей называется зеркальным. Альбедо – доля упавшего излучения, отраженного поверхностью. Поскольку доля отраженного излучения всегда меньше падающего, альбедо всегда меньше 1. Чем больше альбедо, тем большая часть излучения отражена.

Белые тела (например, снег) почти полностью отражают свет, а черные (например, уголь) – почти полностью поглощают.

Самый светлый астероид – 44 Низа – имеет альбедо 0,38, а почти черный астероид – 52 Европа – имеет альбедо 0,03.

6

Рисунок 2.1.2.6. Планета Меркурий отражает в несколько раз больше света, чем каменный уголь. Ее альбедо 0,11