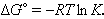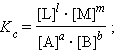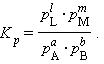Глава 4. Химическая термодинамика
4.7. Химическое равновесие
Для определения величины ΔG в условиях, отличных от стандартных, используют уравнение зависимости изобарно-изотермического потенциала от концентрации и температуры.
Используя соотношения (4.1) и (4.2), получаем:
Рассмотрим вместо небольших, но конечных изменений (ΔG, ΔH, ΔS) бесконечно малые изменения всех параметров, входящих в уравнение (4.3). Тогда оно приобретает вид:
|
|
dG = dU + P dV + V dP – T dS – S dT.
|
(4.4)
|
Подставив в него dU = δQ – δA, получим:
|
|
dG = δQ – δA + P dV + V dP – T dS – S dT.
|
(4.5)
|
Если реакция протекает при постоянной температуре (S dT = 0) и обратимо (ΔQ = T dS), а единственной совершаемой в ходе реакции работой является работа расширения (δА = P dV), то в правой части (4.5) все члены, кроме V dP, взаимно сокращаются или равны нулю. Тогда получаем:
Для одного моля идеального газа V = RT / P и, следовательно,
| |
dG = RT dP / P = RT d (lnP) |
|
Интегрируя, получаем
Это уравнение позволяет, зная молярную энергию Гиббса идеального газа G1 при парциальном давлении P1, вычислить молярную энергию Гиббса G2 при парциальном давлении P2. Хотя уравнение 4.6 выведено для обратимой реакции, оно в равной мере применимо и к необратимым процессам, поскольку G является функцией состояния, и ее изменение не зависят от способа перехода из состояния 1 в состояние 2. Допустив, что состояние 1 является стандартным, а состояние 2 произвольным, уравнение (4.6) можно записать в виде:
где 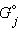 – стандартный изобарно-изотермический потенциал вещества j;
– стандартный изобарно-изотермический потенциал вещества j; 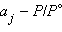 – его активная концентрация (активность).
– его активная концентрация (активность).
Для идеальных растворов активная концентрация определяется как отношение концентрации этого вещества при заданных условиях к его концентрации в стандартном состоянии a = C/C°. Вещества в стандартном состоянии имеют a = 1.
В соответствии с (4.7) энергия Гиббса произвольной химической реакции
равна:
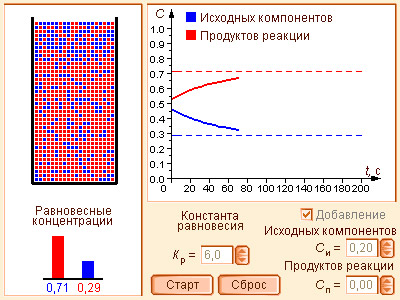
При достижении равновесия (ΔG = 0) уравнение (4.8) принимает вид
где 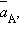
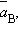

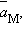 – равновесные значения активных концентраций.
– равновесные значения активных концентраций.
Выражение под знаком логарифма, представляющее собой отношение произведения равновесных активностей продуктов к произведению активностей исходных веществ в степенях их стехиометрических коэффициентов, называется константой равновесия:
|
|
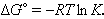 |
(4.9)
|

 |
|
Модель 4.12.
Химическое равновесие
|
Подставив (4.9) в (4.8), получим уравнение, носящее название изотермы Вант-Гоффа:
При определенных условиях активности реагентов могут быть заменены концентрациями или парциальными давлениями. В этих случаях константа равновесия, выраженная через равновесные концентрации Kc или через парциальные давления Kp, принимает вид
|
|
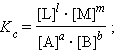 |
(4.11)
|
|
|
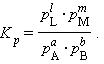 |
(4.12)
|
Уравнения (4.11) и (4.12) представляют собой варианты закона действующих масс (ЗДМ) для обратимых реакций в состоянии равновесия. При постоянной температуре отношение равновесных концентраций (парциальных давлений) конечных продуктов к равновесным концентрациям (парциальным давлениям) исходных реагентов, возведенных соответственно в степени, равные их стехиометрическим коэффициентам, величина постоянная (К. Гульдберг, П. Вааге, 1867 г.).
Для газообразных веществ Kp и Kc связаны соотношением Kp = (RT)ΔnKc, где Δn – разность числа молей начальных и конечных газообразных реагентов.
Константа равновесия определяется при известных равновесных концентрациях реагирующих веществ или по известной ΔG° химической реакции.






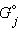 – стандартный изобарно-изотермический потенциал вещества
– стандартный изобарно-изотермический потенциал вещества 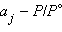 – его активная концентрация (активность).
– его активная концентрация (активность).
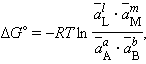
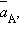
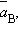

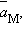 – равновесные значения активных концентраций.
– равновесные значения активных концентраций.