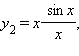Глава 1. Теоретические сведения о функциях
1.3. Числовые функции
1.3.6. Предел функции
Понятие предела функции является одним из самых важных в математике. Дадим два определения этому понятию.
Определение предела по Коши. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для каждого ε > 0 существует δ > 0 такое, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x) – A| < ε.
Определение предела по Гейне. Число A называется пределом функции f (x) в точке a, если эта функция определена в некоторой окрестности точки a за исключением, быть может, самой точки a, и для любой последовательности 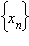 такой, что
такой, что 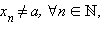 сходящейся к числу a, соответствующая последовательность значений функции
сходящейся к числу a, соответствующая последовательность значений функции 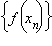 сходится к числу A.
сходится к числу A.
|
|
| График 1.3.6.1. Предел функции y = x2 при x → 2. |
|
|
График 1.3.6.2.Предел функции 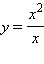 при x → 0. |
Если A – предел функции в точке a, то пишут, что
Определения предела функции по Коши и по Гейне эквивалентны.
|
|
| График 1.3.6.3. Предел функции y = {x (x ≠ 0); 1 (x = 0)} при x → 0 равен 0. |
Предел функции 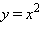 в точке a = 0 равен 0:
в точке a = 0 равен 0:
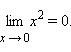 Предел функции
Предел функции
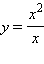 в точке a = 0 также равен 0, хотя эта функция не существует в этой точке (ее знаменатель обращается в нуль). Предел функции
в точке a = 0 также равен 0, хотя эта функция не существует в этой точке (ее знаменатель обращается в нуль). Предел функции
 в точке a = 0 равен 0, хотя значение функции в этой точке f (0) = 1.
в точке a = 0 равен 0, хотя значение функции в этой точке f (0) = 1.
Если функция f (x) имеет предел в точке a, то этот предел единственный.
Число A1 называется пределом функции f (x) слева в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех
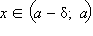 выполняется неравенство
выполняется неравенство 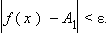
Число A2 называется пределом функции f (x) справа в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех
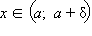 выполняется неравенство
выполняется неравенство 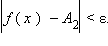
Предел слева обозначается
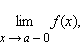 предел справа –
предел справа –
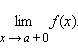 Эти пределы характеризуют поведение функции слева и справа от точки a. Их часто называют односторонними пределами. В обозначении односторонних пределов при x → 0 обычно опускают первый нуль:
Эти пределы характеризуют поведение функции слева и справа от точки a. Их часто называют односторонними пределами. В обозначении односторонних пределов при x → 0 обычно опускают первый нуль:
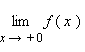 и
и
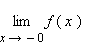 .
Так, для функции
.
Так, для функции
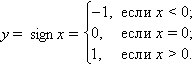
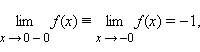
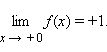
Если для каждого ε > 0 существует такая δ-окрестность точки a, что для всех x, удовлетворяющих условию |x – a| < δ, x ≠ a, выполняется неравенство |f (x)| > ε, то говорят, что функция f (x) имеет в точке a бесконечный предел:
Так, функция
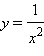 имеет в точке x = 0 бесконечный предел
имеет в точке x = 0 бесконечный предел
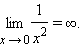 Часто различают пределы, равные +∞ и –∞. Так,
Часто различают пределы, равные +∞ и –∞. Так,
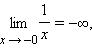
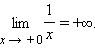
Если для каждого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство |f (x) – A| < ε, то говорят, что предел функции f (x) при x, стремящемся к плюс бесконечности, равен A:
Аналогично формулируется определение предела при x, стремящемся к минус бесконечности:
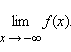 В качестве примера приведем функцию
В качестве примера приведем функцию
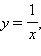 которая стремится на бесконечности к нулю:
которая стремится на бесконечности к нулю:
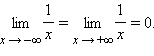
Наконец, запись
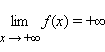 означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) > ε. Запись
означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) > ε. Запись
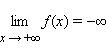 означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) < –ε. Запись
означает, что для любого ε > 0 существует такое δ > 0, что для любого x > δ выполняется неравенство f (x) < –ε. Запись
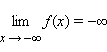 означает, что для любого ε > 0 существует такое δ > 0, что для любого x < –δ выполняется неравенство f (x) < –ε.
означает, что для любого ε > 0 существует такое δ > 0, что для любого x < –δ выполняется неравенство f (x) < –ε.
Если функция f (x) имеет конечный предел в точке a, то существует окрестность точки a, в которой функция f ограничена ( возможно, что в самой точке a функция не определена). При этом, если A ≠ 0, то найдется окрестность точки a, в которой (быть может, за исключением самой точки a) значения функции f имеют тот же знак, что и число A.
Если существует такое δ > 0, что для всех x, принадлежащих δ-окрестности точки a, выполняются неравенства
и если
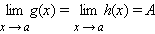 ,
,
|
то существует
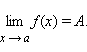
Если существует такое δ > 0, что для всех x, принадлежащих δ-окрестности точки a, справедливо неравенство
и если

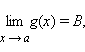 то A ≤ B.
то A ≤ B.
Если функции f (x) и g (x) имеют конечные пределы в точке a, причем
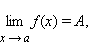
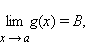 то
то
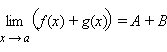 ,
,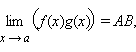
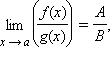 если B ≠ 0 и если g (x) ≠ 0 в δ-окрестности точки a.
если B ≠ 0 и если g (x) ≠ 0 в δ-окрестности точки a.
Из существования пределов f (x) в точке a и g (y) в точке f (a) следует существование предела сложной функции g (f (x)) в точке a.
Для вычисления пределов часто используют так называемые замечательные пределы:
Для доказательства первого предела используется неравенство
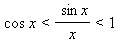 ,
,
|
верное для
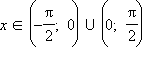
(неравенство sin x < x следует из определения синуса при рассмотрении единичной окружности, а для доказательства неравенства x < tg x необходимо нарисовать ось тангенсов). Для доказательства второго предела используются теорема о пределе монотонной функции и монотонная ограниченная последовательность
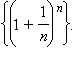
|
Другие важные пределы (при a > 0, a ≠ 1):
следуют из замечательных пределов и свойства предела обратной функции.
Функция α (x) называется бесконечно малой при x → a (здесь a – конечное число или ∞), если
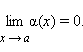 Функция x = 0 является бесконечно малой функцией в каждой точке. Примерами бесконечно малых (на бесконечности) функций являются зависимость силы тяжести от расстояния до притягивающего центра или зависимость скорости движения по параболической орбите от времени.
Функция x = 0 является бесконечно малой функцией в каждой точке. Примерами бесконечно малых (на бесконечности) функций являются зависимость силы тяжести от расстояния до притягивающего центра или зависимость скорости движения по параболической орбите от времени.
- Сумма конечного числа бесконечно малых при x → a функций есть бесконечно малая функция.
- Произведение бесконечно малой при x → a функции на ограниченную в некоторой окрестности точки a функцию есть бесконечно малая при x → a функция.
Если в некоторой окрестности a определены функции f (x), g (x), h (x) такие, что f (x) = g (x) h (x),
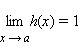 , то функции f (x) и g (x) называются эквивалентными при x → a:
, то функции f (x) и g (x) называются эквивалентными при x → a:
Так, функции 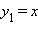 и
и 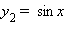 эквивалентны при x → 0, так как
эквивалентны при x → 0, так как
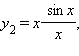 а второй множитель стремится к 1 при x → 0. Другие примеры эквивалентных функций при x → 0:
а второй множитель стремится к 1 при x → 0. Другие примеры эквивалентных функций при x → 0:
|
sin x ~ x
tg x ~ x
arcsin x ~ x
arctg x ~ x
ex – 1 ~ x
ln (1 + x) ~ x
(1 + x)α – 1 ~ α x.
|
При вычислении пределов функций можно использовать понятие эквивалентности.






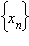 такой, что
такой, что 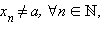 сходящейся к числу
сходящейся к числу 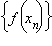 сходится к числу
сходится к числу 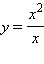 при
при 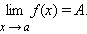
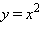 в точке
в точке 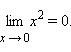
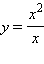

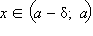
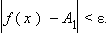
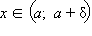
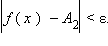
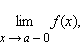
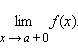
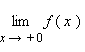
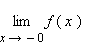 .
.
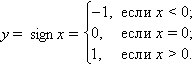
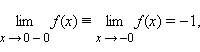
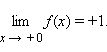
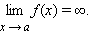
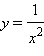
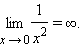
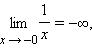
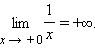
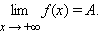
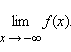
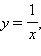
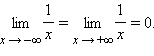
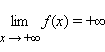
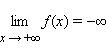
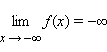
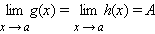 ,
,
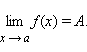

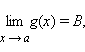
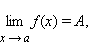
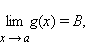
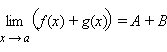
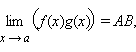
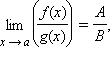
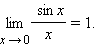
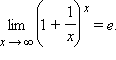
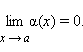
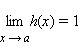
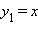 и
и 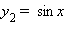 эквивалентны при
эквивалентны при