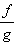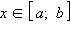Глава 1. Теоретические сведения о функциях
1.3. Числовые функции
1.3.7. Непрерывность функций
Функция f (x), определенная в некоторой окрестности точки a, называется непрерывной в этой точке, если
Пусть функция определена в некоторой окрестности точки a, быть может, за исключением самой точки a. Точка a называется точкой разрыва, если эта функция либо не определена в точке a, либо определена, но не является непрерывной в точке a.
Чаще всего разрыв возникает по двум причинам:
- функция задана различными выражениями на разных участках, и в граничных точках эти выражения имеют различные пределы;
- функция не определена в данной точке.
|
|
| График 1.3.7.1. Эта функция непрерывна в точке A и разрывна в точке B
|
|
|
График 1.3.7.2.На рисунке показана функция
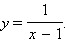
Она разрывна в точке x0 = 1, так как не существует в этой точке.
|
Примером разрывной функции может служить функция зависимости плотности воды в окрестности 0 ºC. Примером непрерывной функции является зависимость площади квадрата от длины его стороны. Подчеркнем еще раз, что непрерывность функции рассматривается только на области ее определения.
Если функция непрерывна в каждой точке некоторого промежутка, то она называется непрерывной на этом промежутке. Большинство функций, изучаемых в элементарной математике, непрерывны на всей области определения. Таковыми являются линейная функция y = kx + b, квадратичная y = ax2 + bx + c, показательная и тригонометрические функции.
Если функции f (x) и g (x) непрерывны в точке x0, то их сумма и произведение также непрерывны в этой точке, а функция
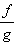 непрерывна в ней при условии, что g (x0) ≠ 0.
непрерывна в ней при условии, что g (x0) ≠ 0.
Отсюда следует, что рациональные функции непрерывны во всех тех точках, в которых их знаменатель не обращается в нуль.
Из непрерывности функции y = f (x) в точке x0 и функции z = g (y) в точке y = f (x0) следует непрерывность сложной функции g (f (x)) в точке x0.
Функцию f (x) называют непрерывной на отрезке [a; b], если она непрерывна в каждой точке интервала (a; b) и, кроме того, непрерывна справа в точке a и слева в точке b.
Теорема Вейерштрасса. Если функция f (x) непрерывна на отрезке [a; b], то она ограничена на этом отрезке и достигает своего наибольшего и наименьшего значения.
 1
|
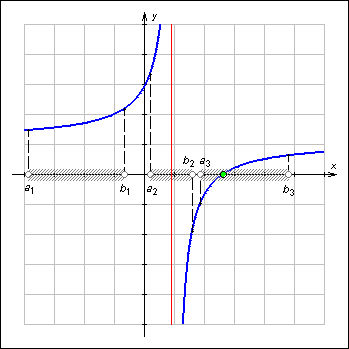
| Рисунок 1.3.7.1. Теорема Коши о нулях непрерывной функции. Только на одном из отрезков – [a3; b3] – имеется нуль функции, так как на этом отрезке функция непрерывна и принимает значения разных знаков на концах
|
Теорема Коши. Если функция f (x) непрерывна на отрезке [a; b] и принимает на его концах значения разных знаков, то на отрезке [a; b] имеется хотя бы один нуль функции f. При этом, если функция строго монотонна на этом отрезке, то она принимает значение 0 лишь один раз.
Теорема о промежуточных значениях.
Если функция f (x) непрерывна на отрезке [a; b] и f (a) ≠ f (b), то для каждого значения y, заключенного между f (a) и f (b), найдется точка
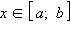 (и возможно, не одна) такая, что f (x) = y.
(и возможно, не одна) такая, что f (x) = y.






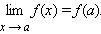
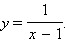 Она разрывна в точке
Она разрывна в точке