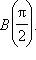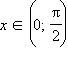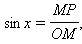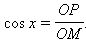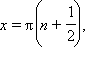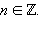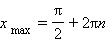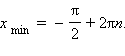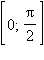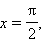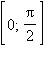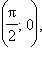Глава 2. Элементарные функции и их графики

2.3. Тригонометрические функции

2.3.2. Синус и косинус

Положение точек на координатной окружности можно задавать не только длиной дуги, но и декартовыми координатами. Построим декартову систему координат с центром в точке O, осью абсцисс, проходящей через начало отсчета A (0), и осью ординат, проходящей через точку 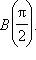За единицу отсчета возьмем радиус этой окружности. Декартовы координаты точки M (x) единичной окружности называются косинусом и синусом числа x:

M (x) = M (cos x; sin x).

Модель 2.9. Координатная окружность

Для 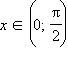определение синуса и косинуса совпадает с геометрическим определением этих понятий, заданных при помощи прямоугольного треугольника OPM. В этом случае

Так как координаты точек окружности единичного радиуса по модулю не превосходят 1, то

|cos x| ≤ 1, |sin x| ≤ 1.

Таким образом, областью значений обеих функций является отрезок [–1; 1].

Ниже приведены значения косинуса и синуса для некоторых значений x:

x 0 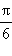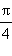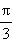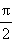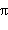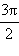0 30° 45° 60° 90° 180° 270° sin x 0 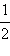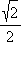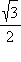1 0 –1 cos x 1 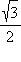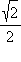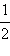0 –1 0

Таблица 2.3.2.1

Функция sin x обращается в нуль при x = πn, функция cos x обращается в нуль при  

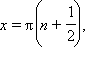
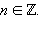
График 2.3.2.1. Графики функций y = sin x и y = cos x.

Функции sin x и cos x непрерывны на всей области определения. Они периодичны; их основной период равен 2π.

Промежутки монотонности и знакопостоянства:

Функция 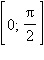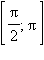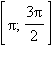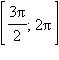sin x Неотрицателен, возрастает от 0 до 1 Неотрицателен, убывает от 1 до 0 Неположителен, убывает от 0 до –1 Неположителен, возрастает от –1 до 0 cos x Неотрицателен, убывает от 1 до 0 Неположителен, убывает от 0 до –1 Неположителен, возрастает от –1 до 0 Неотрицателен, возрастает от 0 до 1

Таблица 2.3.2.2

Синус достигает максимума в точках 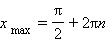и минимумы в точках 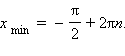Косинус достигает максимума в точках x_max = 2πn, минимума – в точках x_min = π + 2πn.

Функция sin x нечетна, функция cos x четна:

Формулы приведения, позволяющие свести тригонометрические функции от любого аргумента к функциям от углов из промежутка :

cos (x + π) = –cos x cos (π – x) = –cos x sin (x + π) = –sin x sin (π – x) = sin x

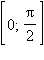Основное тригонометрическое тождество (следствие теоремы Пифагора):

Некоторые тригонометрические формулы приведены в таблице.

График функции y = sin x называется синусоидой, а функции y = cos x – косинусоидой. В обоих случаях достаточно построить графики на отрезке [0; 2π] или [–π; π], а затем периодически продолжать их на всю ось. Более того, достаточно построить график y = sin x на отрезке отразить симметрично относительно оси 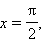а затем отразить получившийся график относительно точки (π; 0). График y = cos x после построения на отрезке 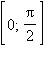нужно отразить относительно точки 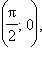а затем получившийся график – относительно оси x = π. Заметим также, что косинусоида получается из синусоиды сдвигом на π/2 влево, поэтому, как правило, используется только термин «синусоида».

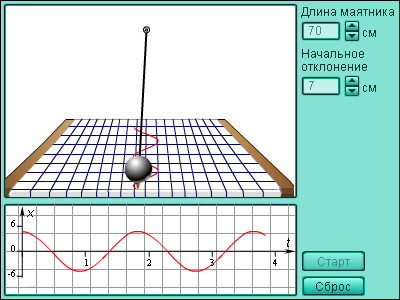
Модель 2.10. Математический маятник

Синус и косинус применяются во многих областях физики и математики. Например, с их помощью удобно описывать гармонические колебания, задаваемые формулами y = A cos (ωx + φ) или y = A sin (ωx + φ). Здесь A – амплитуда, ω – частота, φ – начальная фаза колебаний. Для построения графика гармонического колебания необходимо последовательно выполнить следующие операции над синусоидой:

• сжать к оси ординат с коэффициентом ω,
• перенести вдоль оси абсцисс на φ влево,
• растянуть от оси абсцисс в A раз.

Если мы имеем дело с явлением, в котором одновременно происходят несколько различных колебательных процессов с соизмеримыми периодами, то зависимость колеблющейся величины от времени остается периодической, но график этой зависимости в общем случае уже не является синусоидой. Любую из функций, описывающих эту зависимость, можно представить в виде суммы постоянной составляющей и гармонических колебаний с частотами, кратными

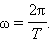
Модель 2.11. Колебания в электрической цепи