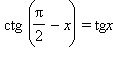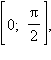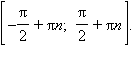Глава 2. Элементарные функции и их графики
2.3. Тригонометрические функции
2.3.3. Тангенс и котангенс
Тангенсом угла x называется отношение синуса этого угла к косинусу этого же угла. Котангенсом угла x называется отношение косинуса этого угла к синусу этого же угла:
Поскольку деление на нуль невозможно, эти функции определены не для всех значений аргумента. Тангенс определен для всех
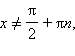
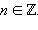 Котангенс определен для всех
Котангенс определен для всех
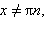
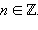 Обе функции непрерывны на всей области определения и имеют разрывы в точках вида
Обе функции непрерывны на всей области определения и имеют разрывы в точках вида
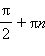 (тангенс) и
(тангенс) и
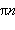 (котангенс).
(котангенс).

 |
|
Модель 2.12.
Тень от солнца
|
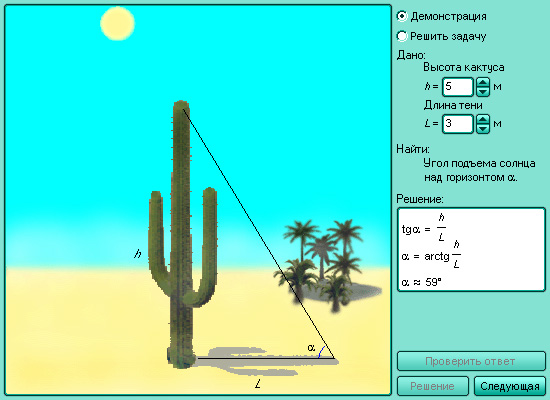
Тангенс и котангенс являются периодическими функциями. Их основной период равен π. Значения этих функций в некоторых точках приведены в таблице.
| x |
0 |
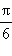 |
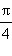 |
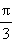 |
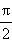 |
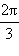 |
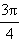 |
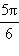 |
| tg x |
0 |
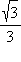 |
1 |
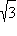 |
– |
 |
–1 |
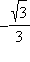 |
| ctg x |
– |
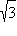 |
1 |
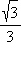 |
0 |
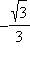 |
–1 |
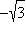 |
|
| Таблица 2.3.3.1 |
Промежутки монотонности и знакопостоянства:
| Функция |
0 |
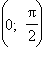 |
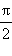 |
 |
| tg x |
0 |
Положителен,
возрастает от 0 до +∞ |
– |
Отрицателен,
возрастает от –∞ до 0 |
| ctg x |
– |
Положителен,
убывает от +∞ до 0 |
0 |
Отрицателен,
убывает от 0 до –∞ |
|
| Таблица 2.3.3.2 |
Функции tg x и ctg x нечетны.
Формулы приведения:
tg (π – x) = –tg x, ctg (π – x) = –ctg x
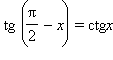 , ,
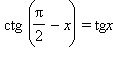 |
Тождества, связанные с тангенсами и котангенсами:
Некоторые тригонометрические формулы приведены в таблице.
|
|
| График 2.3.3.1. Графики функций y = tg x и y = ctg x.
|
Поскольку тангенс и котангенс – нечетные функции, достаточно построить их графики на отрезке
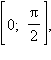 отразить симметрично относительно начала координат и периодически продолжить получившийся график на отрезки
отразить симметрично относительно начала координат и периодически продолжить получившийся график на отрезки
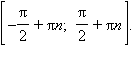






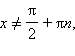
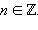
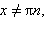
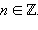
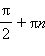
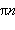


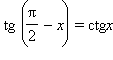 ,
,