Глава 2. Элементарные функции и их графики
2.3. Тригонометрические функции
2.3.1. Координатная окружность
Тригонометрическими называются функции вида y = sin x, y = cos x, y = tg x, y = ctg x и их комбинации.

 |
|
Модель 2.9.
Координатная окружность
|
 1
|
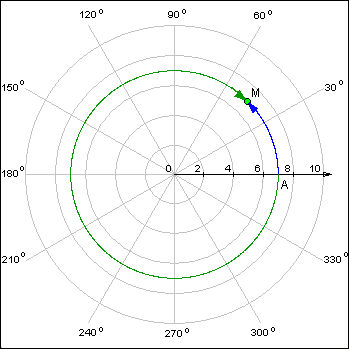
| Рисунок 2.3.1.1. Одной и той же точке можно сопоставить длину дуги, пробегаемой как в положительном, так и в отрицательном направлении
|
Назовем координатной окружность единичного радиуса, на который выбраны начало отсчета A и направление отсчета (обычно в качестве положительного выбирают направление обхода против часовой стрелки). Произвольному числу
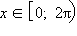 ставится в соответствие точка на окружности M (x) такая, что длина дуги, соединяющей начало отсчета A с этой точкой, равняется x. Если же число x принадлежит промежутку
ставится в соответствие точка на окружности M (x) такая, что длина дуги, соединяющей начало отсчета A с этой точкой, равняется x. Если же число x принадлежит промежутку
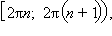
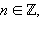 то ему в соответствие ставится точка M (x), длина дуги до которой равняется x – 2πn. Таким образом, всем числам x + 2πn,
то ему в соответствие ставится точка M (x), длина дуги до которой равняется x – 2πn. Таким образом, всем числам x + 2πn,
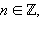 геометрически ставится в соответствие одна и та же точка M (x) координатной окружности.
геометрически ставится в соответствие одна и та же точка M (x) координатной окружности.
|
|
| График 2.3.1.1. Симметрия точек на координатной окружности
|
Точки B (x) и C (–x) симметричны относительно оси OA, где O – центр окружности. Точки B (x) и D (π + x) симметричны относительно центра окружности O.
Центральный угол α (выраженный в радианах) определяется как 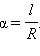 Таким образом, длина дуги, содержащей центральный угол α, равна
Таким образом, длина дуги, содержащей центральный угол α, равна
Отношение длины окружности C к ее диаметру постоянно и равно 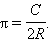 Число π – трансцендентное, π = 3,14159... Используя число π, можно записать выражение для длины окружности:
Число π – трансцендентное, π = 3,14159... Используя число π, можно записать выражение для длины окружности:
Площадь сектора равна
а площадь всего круга (α = 2π) равна S = πR2.









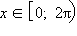
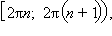
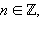
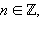
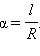 Таким образом, длина дуги, содержащей центральный угол
Таким образом, длина дуги, содержащей центральный угол 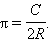 Число
Число 



