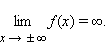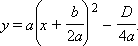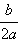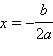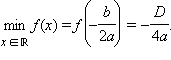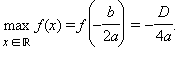Глава 2. Элементарные функции и их графики
2.2. Квадратичная функция
2.2.3. График квадратичной функции
График функции 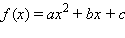 при a ≠ 0 называется параболой. Рассмотрим сначала функцию
при a ≠ 0 называется параболой. Рассмотрим сначала функцию 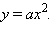 Областью определения этой функции являются все
Областью определения этой функции являются все
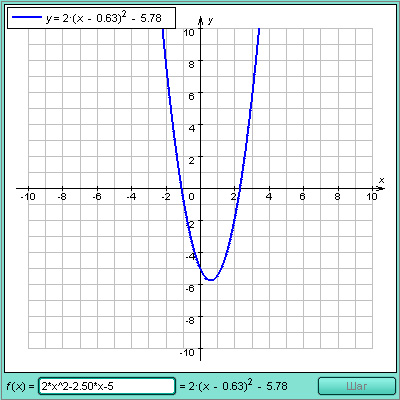
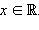 Решив уравнение
Решив уравнение 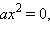 получим x = 0. Итак, единственный нуль этой функции x = 0. Функция
получим x = 0. Итак, единственный нуль этой функции x = 0. Функция 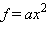 является четной (для любых
является четной (для любых
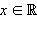
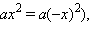 ось OY является ее осью симметрии.
ось OY является ее осью симметрии.
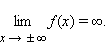
|
|
| График 2.2.3.1. График функции y = ax2, a = 1 > 0.
|
При a > 0 функция убывает на x < 0 и возрастает на x > 0. Точка x = 0 по определению является минимумом функции. Областью значений функции в этом случае является промежуток [0; +∞).
При a < 0 функция возрастает на x < 0 и убывает на x > 0. Точка x = 0 является максимумом функции. Областью значений функции в этом случае является промежуток (–∞; 0].

 |
|
Модель 2.6.
Построение параболы
|
График функции f (x) = ax2 + bx + c легко построить из графика функции y = x2 геометрическими преобразованиями, используя формулу
Для этого нужно растянуть график y = x2 в a раз от оси OX, при необходимости отразив его относительно оси абсцисс, а затем сместить получившийся график на
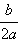 влево и на
влево и на
 вниз (если какое-либо из этих чисел меньше нуля, то соответствующее смещение нужно производить в противоположную сторону).
вниз (если какое-либо из этих чисел меньше нуля, то соответствующее смещение нужно производить в противоположную сторону).
 1
|
| Рисунок 2.2.3.1. Парабола является одним из конических сечений
|
Точка
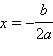 является точкой экстремума и называется вершиной параболы. Если a > 0, то в этой точке достигается минимум функции, и
является точкой экстремума и называется вершиной параболы. Если a > 0, то в этой точке достигается минимум функции, и
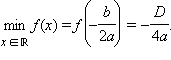 Если a < 0, то в этой точке достигается максимум функции, и
Если a < 0, то в этой точке достигается максимум функции, и
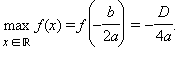
Функция f (x) = ax2 + bx + c при b = 0 является четной, а в общем случае уже не является ни четной, ни нечетной.

 |
|
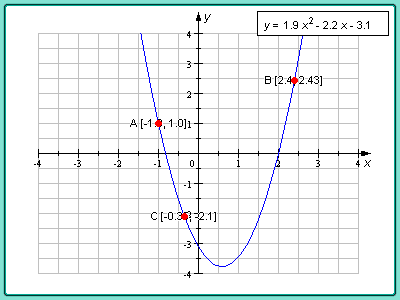
Модель 2.8.
Построение параболы по трем точкам
|






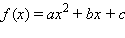 при
при 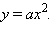 Областью определения этой функции являются все
Областью определения этой функции являются все
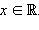
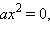 получим
получим 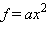 является четной (для любых
является четной (для любых
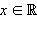
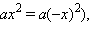 ось
ось