Глава 2. Элементарные функции и их графики

2.2. Квадратичная функция

Назад Вперед
Назад Вперед

2.2.2. Квадратное уравнение

Уравнение
ax2 + bx + c = 0,
где a ≠ 0, называется квадратным уравнением.

Выделив полный квадрат, получим уравнение Если то отсюда следует, что
или

Мы получили формулу корней квадратного уравнения (формулу Виета).

1
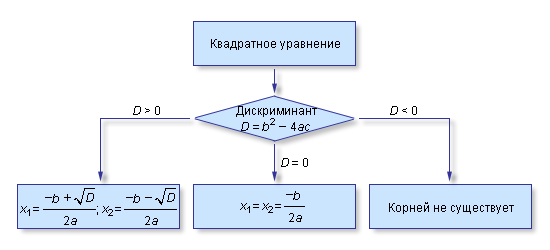
Рисунок 2.2.2.1.
Алгоритм поиска корней квадратного уравнения

При D > 0 существуют два корня x1 и x2. При D = 0 корни квадратного уравнения совпадают: x1 = x2. Наконец, при D < 0 равенство невозможно, и корней у квадратного уравнения не существует.

Если D ≥ 0, то квадратичную функцию можно разложить на множители: Таким образом
y = a (x – x1) (x – x2),
где Если D = 0, то  Если D < 0, то квадратный трехчлен нельзя разложить на множители.

Модель 2.5. Движение по параболе

Теорема Виета. Для того чтобы числа x1 и x2 были корнями уравнения ax2 + bx + c = 0 (a ≠ 0), необходимо и достаточно, чтобы выполнялись равенства:

Доказательство

  1. Необходимость. Пусть числа и являются корнями уравнения  (a ≠ 0). Тогда   Имеем   

  2. Достаточность. Пусть имеется система Из первого равенства Подставляя это значение во второе равенство, получим откуда Значит, число является корнем квадратного уравнения  Аналогично доказывается, что – также корень этого уравнения.

Назад Вперед
Наверх

Включить/Выключить фоновую музыкуВключить/Выключить звуки событий