

 |
 |
В природе и жизни человека встречается большое количество процессов, в которых некоторые величины изменяются так, что их отношение данной величины через равные промежутки времени не зависит от времени. Среди таковых можно назвать радиоактивный распад веществ, рост суммы на счету в банке и др. Все эти процессы описываются показательной функцией.
Пусть
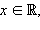
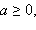
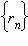 – последовательность рациональных чисел, сходящихся к
– последовательность рациональных чисел, сходящихся к 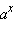 как предел
как предел
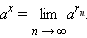 |
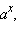
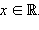
|
|
|
| График 2.4.3.1. График показательной функции 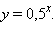 |
Данный предел не зависит от выбора последовательности 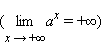
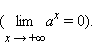
|
|
|
| График 2.4.3.2. График экспоненциальной функции |
Особое значение в приложениях имеет показательная функция, в качестве основания которой используют число 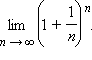
Определенная так функция называется экспоненциальной или просто экспонентой и обозначается
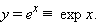 |

 |
|
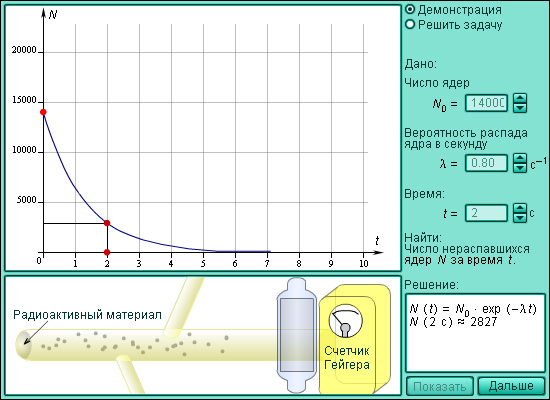
Модель 2.16.
Радиоактивный распад
|
В заключение приведем пример из физики. Количество радиоактивного вещества, оставшегося к моменту
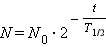 . .
|
Здесь 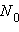 – первоначальное количество вещества,
– первоначальное количество вещества, 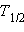 – период полураспада.
– период полураспада.
 |
 |
 |

