Глава 2. Элементарные функции и их графики
2.4. Другие элементарные функции
2.4.2. Степенная функция
Степенная функция с натуральным показателем 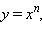
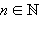 непрерывна на множестве действительных чисел. Если n нечетное, то эта функция строго возрастает и потому обратима. Обратной к ней является функция
непрерывна на множестве действительных чисел. Если n нечетное, то эта функция строго возрастает и потому обратима. Обратной к ней является функция
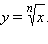 Степенная функция с четным показателем необратима. Однако если сузить ее область определения до области неотрицательных чисел, то обратной к ней функцией также будет
Степенная функция с четным показателем необратима. Однако если сузить ее область определения до области неотрицательных чисел, то обратной к ней функцией также будет
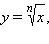 x ≥ 0. На множестве (–∞; 0) функцией, обратной к функции
x ≥ 0. На множестве (–∞; 0) функцией, обратной к функции 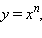 (n – натуральное четное число) будет
(n – натуральное четное число) будет
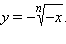
|
|
| График 2.4.2.1. Степенная и обратная ей функции
|
Итак, если x > 0, то при любом натуральном n функция 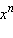 обратима, а обратная к ней функция обозначается как
обратима, а обратная к ней функция обозначается как
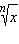 или
или
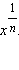 Функция
Функция
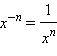 также определена и непрерывна на множестве положительных чисел.
также определена и непрерывна на множестве положительных чисел.
Пусть
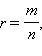
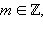
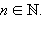 Тогда степенной функцией с рациональным показателем
Тогда степенной функцией с рациональным показателем 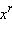 называют функцию
называют функцию
Эта функция определена на множестве чисел x > 0 и непрерывна на всей области определения, строго возрастает при r > 0
(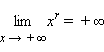 )
и строго убывает при r < 0
(
)
и строго убывает при r < 0
(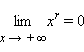 ).
Перечислим некоторые свойства рациональных степеней.
).
Перечислим некоторые свойства рациональных степеней.
 |
a > 0 |
| ar > 1 |
a > 1, r > 0 или 0 < a < 1, r < 0 |
| ar < 1 |
a > 1, r < 0 или 0 < a < 1, r > 0 |
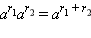 |
a > 0 |
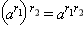 |
a > 0 |
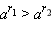 |
a > 1, r1 > r2 |
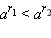 |
0 < a < 1, r1 > r2 |
|
| Таблица 2.4.2.1 |
Степенная функция с вещественным показателем при x > 0 определяется формулой:
(см. определение логарифма). Эта функция непрерывна и строго возрастает (при α > 0) или строго убывает (при α < 0) на всей области определения. Ее областью значений являются все положительные числа.






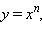
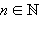 непрерывна на множестве действительных чисел. Если
непрерывна на множестве действительных чисел. Если 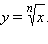
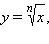
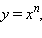
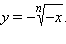
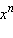 обратима, а обратная к ней функция обозначается как
обратима, а обратная к ней функция обозначается как
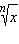
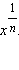
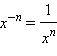
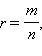
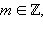
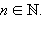
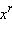 называют функцию
называют функцию
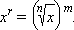
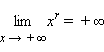 )
)
 ).
).




