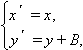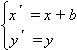Глава 1. Теоретические сведения о функциях

1.4. Преобразование графиков функций

1.4.1. Параллельный перенос

Пусть имеется график функции y = f (x). Зададимся целью построить график функции y = f₁ (x), где f₁ (x) = f (x) + B. Ясно, что области определения этих функций совпадают. Пусть A (x₀; y₀) – точка на графике функции y = f (x). Соответствующая ей точка A′ (x₀; y₁) с той же абсциссой имеет координаты A′ (x₀; y₀ + B). Точка A′ получается из точки A сдвигом на B вертикально вверх, если B > 0, и на |B| вниз, если B < 0. Обобщая это рассуждение на все точки, приходим к выводу, что график функции y = f (x) + B получается из графика функции y = f (x) параллельным переносом вдоль оси OY на B вверх, если B > 0, и на |B| вниз, если B < 0.

Алгебраически для каждой точки графика это можно записать системой
где x и y – координаты какой-либо точки старого графика, x′ и y′ – соответствующей ей точки нового.

Аналогичным образом можно построить график функции y = f (x – b). Точка A′ (x′; y′) нового графика имеет такую же ординату, как и точка A (x; y), если x′ = x + b. Таким образом, чтобы построить точку A′, нужно сместить точку A вправо, если b > 0, и влево, если b < 0.

Модель 1.13. Параллельный перенос графиков

График функции y = f (x – b) получается из графика функции y = f (x) параллельным переносом вдоль оси OX на b вправо, если b > 0, и на |b| влево, если b < 0.

Алгебраически это записывается системой:

Область определения функции, соответствующей новому графику, также смещается на a по отношению к области определения функции, задающей старый график.

В общем случае график функции y = f (x – b) + B получается из графика функции y = f (x) параллельным переносом, при котором начало координат O (0, 0) переходит в точку O′ (b, B). Обычно находят точку O′ и проводят через нее вспомогательные координатные оси, относительно которых строят график функции y = f (x).