Решение.
Функция y = 2 cos x непрерывна на всей числовой оси, а функция f (x) определена только при тех значениях, при которых cos x > 0. Значит, функция g (x) определена только при x > 0.
Построив рядом график функции y = 2 cos x, заметим, что точки пересечения графика функции f (x) с осью абсцисс совпадают с точками пересечения с этой осью косинусоиды. Отсюда можно сделать вывод, что g (0) = 0.
Из графика также можно выяснить, что при тех x, при которых 2 cos x < 1, функция g (x) > 2 cos x (т.е. увеличивает значение своего аргумента); при тех x, при которых 2 cos x > 1, функция g (x) < 2 cos x (т.е. уменьшает значение своего аргумента). Таким образом, g (1) = 1.
Итак, при 0 < x < 1 график функции g (x) находится над графиком функции y = x, при x > 1 – под ним. Такое поведение характерно для степенной функции y = xa с показателем
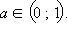 Т.к.
Т.к.
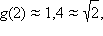 можно предположить, что a = 1/2.
можно предположить, что a = 1/2.
Построив график функции
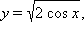 убеждаемся, что он совпадает с графиком функции f (x). Значит, наши предположения были правильными, и
убеждаемся, что он совпадает с графиком функции f (x). Значит, наши предположения были правильными, и
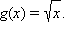


 Задачи
Задачи

 4 из 4
4 из 4
