Выпуклость функции и точки перегиба
Задачи с решениями
Найдите точки перегиба функции
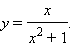
Решение
Функция определена на всей числовой оси. Ее вторая производная равна
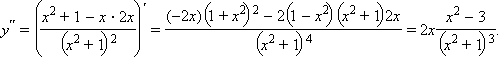Нули второй производной подозрительны на перегиб; решая неравенство
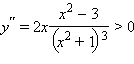методом интервалов, получаем, что на промежутках
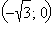и
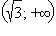функция выпукла вниз. Аналогично, из уравнения
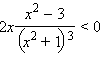следует, что на промежутках
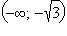и
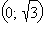функция выпукла вверх. Точки 0,
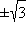являются точками перегиба.
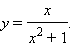
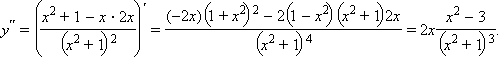
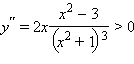
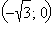
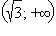
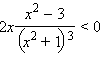
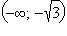
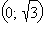
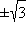
3 из 4
 |
