

 Задачи с решениями
Задачи с решениями

Нарисуйте эскиз графика функции
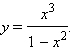
Функция определена при 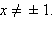 При
При 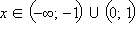 и отрицательные – при
и отрицательные – при 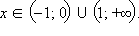 Функция нечетна.
Функция нечетна.
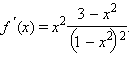 Функция
Функция 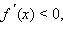 т. е.
т. е. 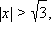 и возрастает при
и возрастает при 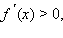 т. е.
т. е. 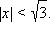 Критическими точками функции являются точки 0, ±1,
Критическими точками функции являются точки 0, ±1, 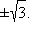 В точках
В точках 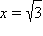 производная меняет знак с «+» на «–» – это точка максимума. Точка
производная меняет знак с «+» на «–» – это точка максимума. Точка 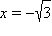 является точкой минимума. Окончательно,
является точкой минимума. Окончательно, 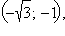
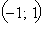 и
и 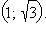
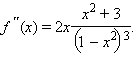
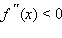 при
при 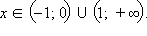 Таким образом, функция выпукла вверх при
Таким образом, функция выпукла вверх при 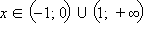 и выпукла вниз при
и выпукла вниз при 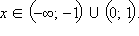
Вертикальными асимптотами функции являются прямые 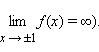 Найдем наклонную асимптоту функции. При
Найдем наклонную асимптоту функции. При 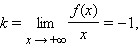
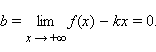 Прямая
Прямая
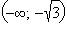 |
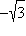 |
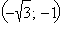 |
0 | 1 | 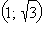 |
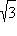 |
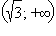 |
||||
| + | 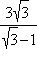 |
+ | Не сущ. | – | 0 | + | Не сущ. | – | 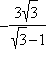 |
– | |
| – | 0 | + | Не сущ. | + | 0 | + | Не сущ. | + | 0 | – | |
| + | + | + | Не сущ. | – | 0 | + | Не сущ. | – | – | – | |
| Прим. | Min | Асимптота | Стац. точка | Асимптота | Max |
Вычислим значение функции в нескольких контрольных точках.
| 2 | 3 | 4 | |
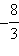 |
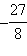 |
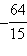 |
График функции изображен на рисунке.
 2 из 4
2 из 4
 |