

 Задачи с решениями
Задачи с решениями

Постройте график функции
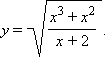
Область определения функции можно найти из неравенства 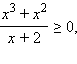 откуда
откуда 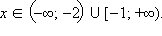 На области определения функция принимает только неотрицательные значения. Нулями функции являются точки 0 и –1.
На области определения функция принимает только неотрицательные значения. Нулями функции являются точки 0 и –1.
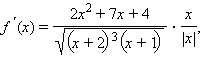 при
при 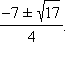 Решая неравенство
Решая неравенство 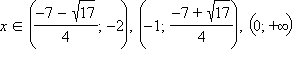 и убывает при
и убывает при 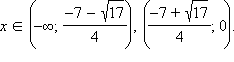 Таким образом, точки
Таким образом, точки 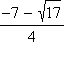 и 0 являются минимумами функции, а точка
и 0 являются минимумами функции, а точка 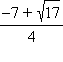 – максимумом. В точке
– максимумом. В точке
Вертикальной асимптотой к графику функции является прямая
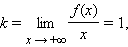
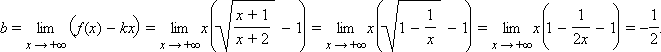
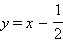 является наклонной асимптотой. Аналогично при отрицательных
является наклонной асимптотой. Аналогично при отрицательных 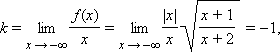
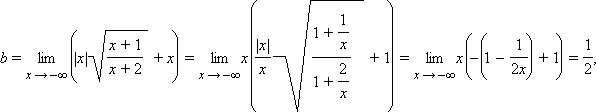
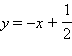 является наклонной асимптотой.
является наклонной асимптотой.
Сведем полученные данные в таблицу.
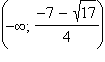 |
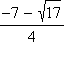 |
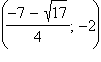 |
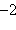 |
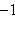 |
|
| + | ≈4.2 | + | ∞ | 0 | |
| – | 0 | + | Не сущ. | + | |
| Прим. | Минимум | Асимптота |
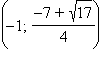 |
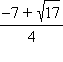 |
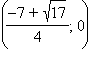 |
0 | 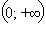 |
|
| + | ≈0.34 | + | 0 | + | |
| + | 0 | – | Не сущ. | + | |
| Прим. | Максимум | Минимум |
Уточним график функции, вычислив
| –3 | 1 | 2 | 3 | |
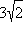 |
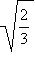 |
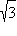 |
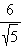 |
Кроме того, заметим, что
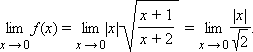
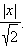
График функции изображен на рисунке.
 3 из 4
3 из 4
 |