Решение.
Так как указанные в условии задачи числа являются длинами сторон треугольника, то все они положительны и удовлетворяют неравенству треугольника:
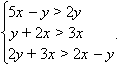 Положительность всех трех чисел приводит к тому, что нас интересуют только точки из первой координатной четверти, лежащие под прямой y = 2x. Система же неравенств эквивалентна системе
Положительность всех трех чисел приводит к тому, что нас интересуют только точки из первой координатной четверти, лежащие под прямой y = 2x. Система же неравенств эквивалентна системе
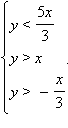 Таким образом, фигурой Ф являются точки первой координатной четверти, лежащие между прямыми y = x и
Таким образом, фигурой Ф являются точки первой координатной четверти, лежащие между прямыми y = x и
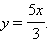
Неравенство
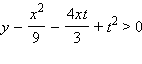 верно при любых t тогда и только тогда, когда
верно при любых t тогда и только тогда, когда
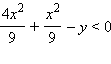 или
или
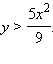 Соответственно, интересующие нас точки фигуры Ф лежат над параболой
Соответственно, интересующие нас точки фигуры Ф лежат над параболой
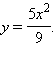
Указанная парабола пересекается с прямой
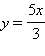 в точках O (0; 0) и A (3; 5), а с прямой y = x в точках O (0; 0) и C
в точках O (0; 0) и A (3; 5), а с прямой y = x в точках O (0; 0) и C
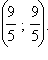 Таким образом, площадь фигуры Ψ равна S = S1 – S2 – S3, где S1 – площадь прямоугольного треугольника OAB, S2 – площадь прямоугольного треугольника OCD, S3 – площадь криволинейной трапеции ACDBE. Подставляя численные значения, получаем
Таким образом, площадь фигуры Ψ равна S = S1 – S2 – S3, где S1 – площадь прямоугольного треугольника OAB, S2 – площадь прямоугольного треугольника OCD, S3 – площадь криволинейной трапеции ACDBE. Подставляя численные значения, получаем
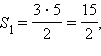
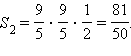 Площадь трапеции легко найти интегрированием:
Площадь трапеции легко найти интегрированием:
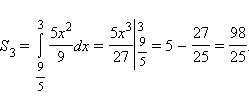
Таким образом,
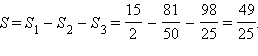
function showUserAnswer(){
testSolution='

 Задачи
Задачи

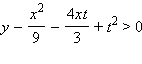
 3 из 6
3 из 6
