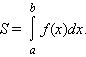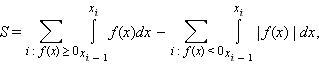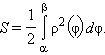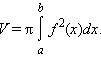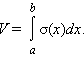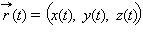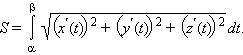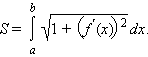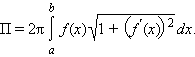Глава 3. Дифференцирование и интегрирование функций

3.4. Определенный интеграл

3.4.4. Геометрические приложения определенного интеграла

1. Площадь плоской фигуры.

Площадь криволинейной трапеции, ограниченной неотрицательной функцией f (x), осью абсцисс и прямыми x = a, x = b, определяется как

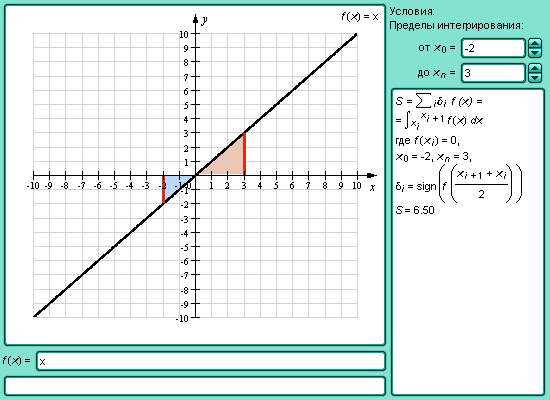
Модель 3.11. Площадь криволинейной трапеции

Площадь фигуры, ограниченной функцией f (x), пересекающей ось абсцисс, определяется формулой
где x_i – нули функции. Другими словами, чтобы вычислить площадь этой фигуры, нужно разбить отрезок [a; b] нулями функции f (x) на части, проинтегрировать функцию f по каждому из получившихся промежутков знакопостоянства, сложить отдельно интегралы по отрезкам, на которых функция f принимает разные знаки, и вычесть из первого второе.

2. Площадь криволинейного сектора.

1

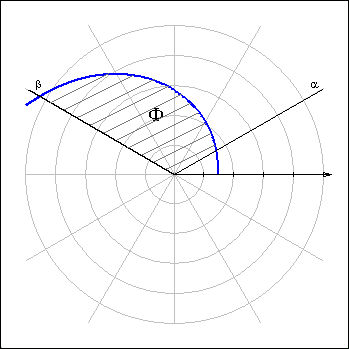
Рисунок 3.4.4.1. Площадь криволинейного сектора

Рассмотрим кривую ρ = ρ (φ) в полярной системе координат, где ρ (φ) – непрерывная и неотрицательная на [α; β] функция. Фигура, ограниченная кривой ρ (φ) и лучами φ = α, φ = β, называется криволинейным сектором. Площадь криволинейного сектора равна

3. Объем тела вращения.

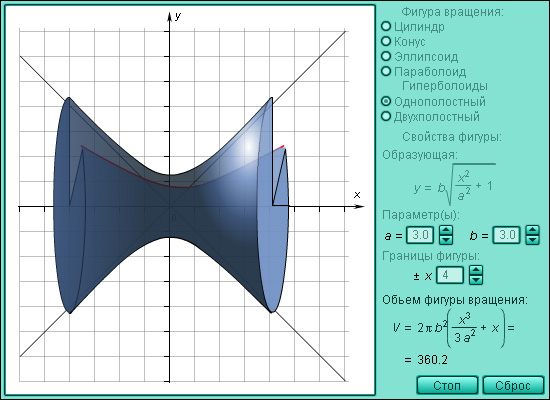
Модель 3.12. Объем тела вращения

Пусть тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной непрерывной на отрезке [a; b] функцией f (x). Его объем выражается формулой

2

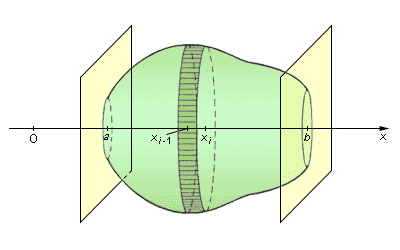
Рисунок 3.4.4.2. К задаче о нахождении объема тела по площади поперечного сечения

Пусть тело заключено между плоскостями x = a и x = b, а площадь его сечения плоскостью, проходящей через точку x, – непрерывная на отрезке [a; b] функция σ (x). Тогда его объем равен

4. Длина дуги кривой.

Пусть задана кривая 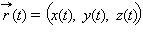Тогда длина ее участка, ограниченного значениями t = α и t = β выражается формулой

3

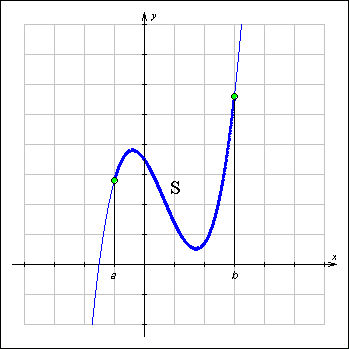
Рисунок 3.4.4.3. Длина дуги плоской кривой

В частности, длина плоской кривой, задаваемой на координатной плоскости OXY уравнением y = f (x), a ≤ x ≤ b, выражается формулой

5. Площадь поверхности вращения.

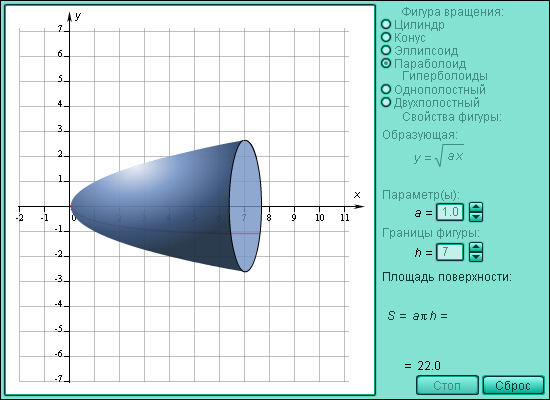
Модель 3.13. Площадь поверхности вращения