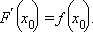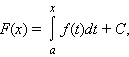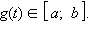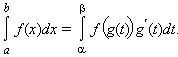Глава 3. Дифференцирование и интегрирование функций
3.4. Определенный интеграл
3.4.3. Формула Ньютона – Лейбница
Если функция f (x) интегрируема на [a; b], то для любого
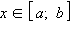 существует интеграл
существует интеграл
который называется
интегралом с переменным верхним пределом.
Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке.
Если функция f интегрируема на [a; b] и непрерывна в
 то функция F (x) дифференцируема в
то функция F (x) дифференцируема в 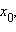 причем
причем
Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида
где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.
Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:
Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).
Пусть f (x) непрерывна на [a; b], g (t) имеет непрерывную производную на [α; β],
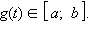 Тогда если a = g (α), b = g (β), то справедлива формула замены переменной в определенном интеграле:
Тогда если a = g (α), b = g (β), то справедлива формула замены переменной в определенном интеграле:
Если функции u (x) и v (x) имеют на [a; b] непрерывные производные, то справедлива формула интегрирования по частям:







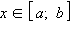
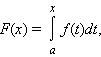

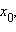 причем
причем