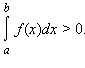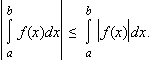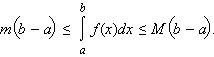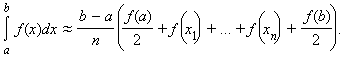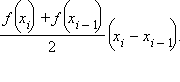Глава 3. Дифференцирование и интегрирование функций
3.4. Определенный интеграл
3.4.2. Свойства определенного интеграла
Доопределим понятие интеграла при a ≥ b следующими равенствами:
Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.
- Если функция интегрируема на [a; b], то она интегрируема на любом отрезке
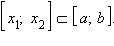
-
Для любых a, b и c
- Интеграл обладает свойством линейности: для любых функций f (x) и g (x) и любой постоянной A
- Если f (x) и g (x) интегрируемы на [a; b], то f (x) · g (x) также интегрируема на этом отрезке.
-
Если f (x) – периодическая функция с периодом T, то для любого a

 |
|
Модель 3.10.
Свойства определенного интеграла
|
Для определенных интегралов верны также следующие оценки (предполагается, что функции f и g интегрируемы на [a; b]).
- Если f (x) ≥ g (x), то
В частности, если f (x) ≥ 0, то
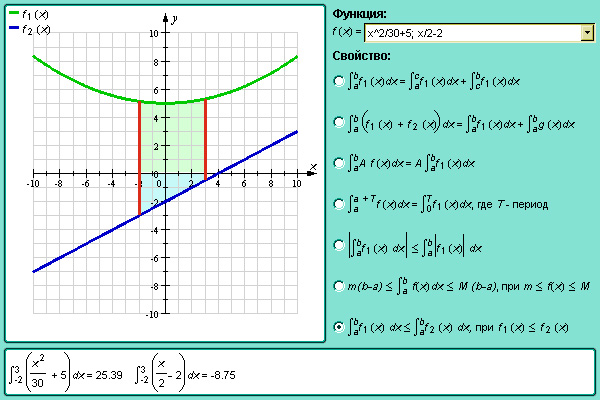
- Если f (x) ≥ 0 для любого
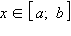 и существует
и существует
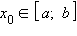 такое, что
такое, что 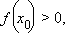 причем f (x) непрерывна в
причем f (x) непрерывна в 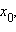 то
то
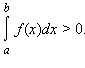
- |f (x)| интегрируема на [a; b], причем
- Если на отрезке [a; b] m ≤ f (x) ≤ M, то
 1
|
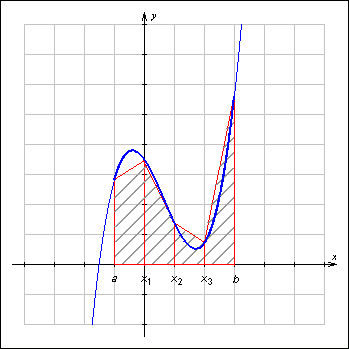
| Рисунок 3.4.2.1. Численное вычисление определенного интеграла при помощи формулы трапеций
|
Для вычисления определенных интегралов на компьютере нередко используют приближенную формулу трапеций:
Ее смысл состоит в том, что криволинейные трапеции заменяются обычными, площадь каждой из которых равна
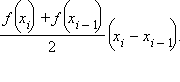






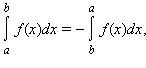
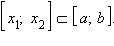
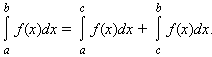

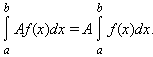
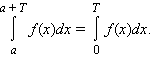


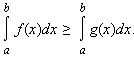
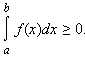
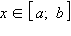
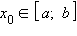
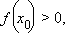 причем
причем 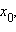 то
то