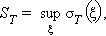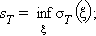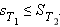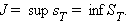Глава 3. Дифференцирование и интегрирование функций
3.4. Определенный интеграл
3.4.1. Определенный интеграл
 1
|
| Рисунок 3.4.1.1. Определение криволинейной трапеции
|
Пусть функция f (x) непрерывна и не меняет знак на отрезке [a; b]. Плоскую фигуру Ф, ограниченную графиком функции f (x), осью абсцисс и прямыми x = a и x = b, называют криволинейной трапецией.
В курсе геометрии было введено понятие площади фигуры S (Ф). Напомним, что площадь обладает следующими свойствами:
- площадь любой фигуры неотрицательна: S (Ф) ≥ 0;
- равные фигуры имеют равные площади: если Ф1 = Ф2, то S (Ф1) = S (Ф2);
- площадь фигуры равна сумме площадей ее частей;
- площадь квадрата со стороной 1 равна единице.
 2
|
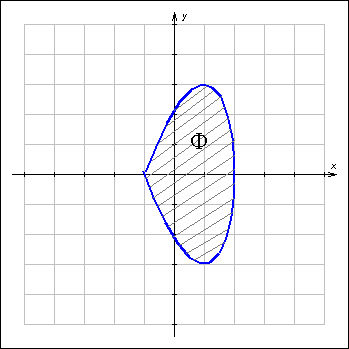
| Рисунок 3.4.1.2. Площадь фигуры Ф
|
В каждую фигуру можно вписать множество равных маленьких квадратов, не имеющих общих внутренних точек и целиком лежащих внутри фигуры Ф. Пусть сумма их площадей равняется sT. Точно так же можно построить такое множество квадратов, которое полностью покрывает фигуру Ф. Обозначим сумму их площадей буквой ST. Очевидно, что sT ≤ ST.
Можно доказать, что если неотрицательная функция f (x) непрерывна на отрезке [a; b], то ее криволинейная трапеция имеет площадь S (Ф), которая подчиняется неравенству sT ≤ S (Ф) ≤ ST, причем sT и ST стремятся к S (Ф) при неограниченном уменьшении площади каждого квадрата. Этот предел S (Ф) не зависит от способа дробления фигуры Ф на квадраты.
Рассмотрим непрерывную и неотрицательную на [a; b] функцию f (x). Разобьем отрезок [a; b] на n отрезков точками x1,..., xn–1. Проведем через эти точки прямые, перпендикулярные оси абсцисс. Тогда криволинейная трапеция Ф, соответствующая графику функции y = f (x), разобьется на n частей, каждая из которых также является криволинейной трапецией.
Обозначим Δxi = xi – xi–1, x0 = a, xn = b и выберем каким-нибудь образом точки
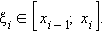 Произведение Δxi · f (ξi) является площадью прямоугольника, ограниченного осью абсцисс, прямыми x = xi–1 и x = xi и горизонтальной прямой y = f (ξi). Суммарная площадь ступенчатой фигуры, являющейся объединением всех прямоугольников, равна
Произведение Δxi · f (ξi) является площадью прямоугольника, ограниченного осью абсцисс, прямыми x = xi–1 и x = xi и горизонтальной прямой y = f (ξi). Суммарная площадь ступенчатой фигуры, являющейся объединением всех прямоугольников, равна
Она зависит от выбора количества n прямоугольников и точек ξi. При достаточно мелком разбиении эта ступенчатая фигура будет мало отличаться от исходной фигуры Ф в том смысле, что можно доказать существование предела
который и принимается равным площади криволинейной трапеции Ф.
Число J называется определенным интегралом от функции f (x) на отрезке [a; b], если для любого ε > 0 существует такое
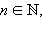 что для разбиения отрезка [a; b] на равные части n точками и для любого выбора точек
что для разбиения отрезка [a; b] на равные части n точками и для любого выбора точек
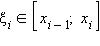 выполняется неравенство
выполняется неравенство
Заметим, что в этом определении предполагается, что функция может быть как положительной, так и отрицательной.
Если число J существует, то функция f (x) называется интегрируемой на отрезке [a; b]. Определенный интеграл обозначается
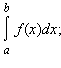 числа a и b называются пределами интегрирования.
числа a и b называются пределами интегрирования.
Если функция f (x) интегрируема на отрезке [a; b], то она ограничена на этом отрезке.
Обратное, вообще говоря, неверно. Так, функция Дирихле
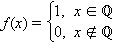 ограничена на любом отрезке, но не интегрируема на нем.
ограничена на любом отрезке, но не интегрируема на нем.
Если функция непрерывна на отрезке, то она интегрируема на нем.
Если функция определена на отрезке и монотонна, то она интегрируема на нем.
Выберем на отрезке 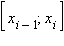 максимальное и минимальное значения функции f (x):
максимальное и минимальное значения функции f (x):
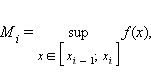
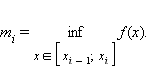 Обозначим через T некоторое разбиение отрезка [a; b] точками
Обозначим через T некоторое разбиение отрезка [a; b] точками 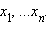
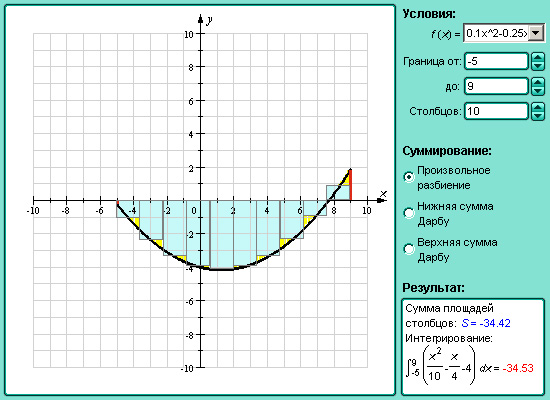
Верхней суммой Дарбу называется выражение
Нижней суммой Дарбу называется

 |
|
Модель 3.9.
Определенный интеграл
|
Свойства сумм Дарбу (здесь
 ):
):
- для любых ξ справедливы неравенства
sT ≤ σT (ξ) ≤ ST;
- справедливы равенства
- при увеличении числа отрезков n нижняя сумма Дарбу не уменьшается, а верхняя – не увеличивается;
- для любых разбиений T1 и T2
Если функция интегрируема на отрезке, то ее определенный интеграл на этом отрезке








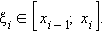
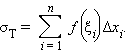

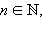
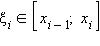
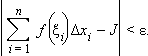
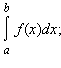
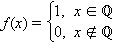
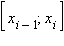 максимальное и минимальное значения функции
максимальное и минимальное значения функции 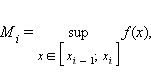
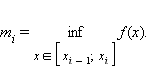
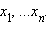

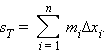


 ):
):