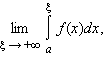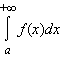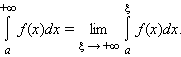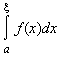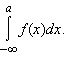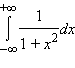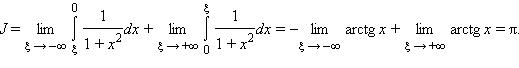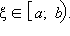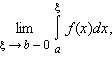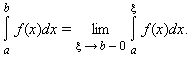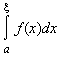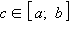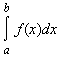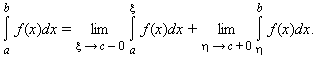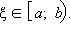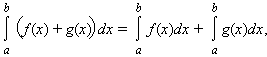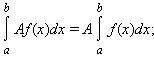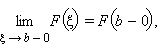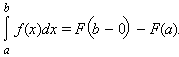Глава 3. Дифференцирование и интегрирование функций

3.4. Определенный интеграл

3.4.6. Несобственные интегралы

Определенный интеграл был введен для ограниченных на отрезке функций. Естественно распространить это понятие на случай бесконечных промежутков и бесконечно больших функций.

Пусть f (x) определена при x ≥ a и интегрируема на отрезке [a; ξ], где ξ ≥ a. Если существует конечный предел 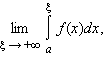то говорят, что функция f интегрируема в несобственном смысле на промежутке [a; +∞), а несобственный интеграл 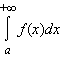сходится:

Если 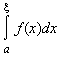не имеет конечного предела при ξ → +∞, то говорят, что несобственный интеграл расходится.

Аналогично определяется несобственный интеграл

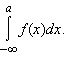
Так, интеграл 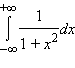сходится и равен 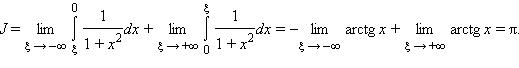Этот ответ можно интерпретировать как площадь фигуры, ограниченной графиком функции и осью OX.

Пусть функция f (x) определена на конечном промежутке [a; b) и интегрируема на отрезке [a; ξ] при любом 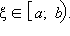Если существует конечный предел 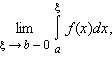то говорят, что несобственный интеграл от функции f (x) на промежутке [a; b) сходится:

Если 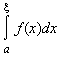не имеет конечного предела при ξ → b, то говорят, что несобственный интеграл расходится.

Аналогично определяется несобственный интеграл для функции, определенной на (a; b].

Если функция f определена на отрезке [a; b] за исключением точки 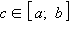и интегрируема на отрезках [a; ξ] и [η; b] при любых ξ и η таких, что a ≤ ξ < c < η ≤ b, то несобственный интеграл от функции f на промежутке [a; b] обозначается 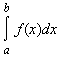и равен

В дальнейшем без ограничения общности будем предполагать, что функция f определена на [a; b), где a – конечная точка, b – конечная точка либо +∞, и функция f интегрируема на [a; ξ] при любом 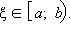В этих предположениях несобственные интегралы обладают следующими свойствами:

• линейность несобственного интеграла:
  
  
• формула Ньютона – Лейбница: если существует конечный предел 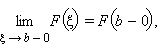то