Глава 2. Элементарные функции и их графики

Модель 2.7.  Жидкость во вращающемся сосуде

Свободная поверхность жидкости во вращающемся сосуде принимает форму параболоида. Действительно, рассмотрим частицу воды на поверхности жидкости. Условие ее равновесия определяется уравнениями 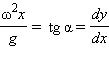mg = N · cos α и mω²x = N · sin α, где m – масса частицы, ω – угловая скорость вращения сосуда, x – координата частицы жидкости, α – угол наклона свободной поверхности жидкости к горизонтали. Разделив второе уравнение на первое, получим (последнее равенство записано в соответствии с геометрическим смыслом производной). Это уравнение сводится к уравнению 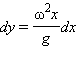, откуда интегрированием получаем 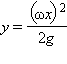. Отсюда следует, что сечение фигуры, образованной свободной поверхностью жидкости, плоскостью z = 0 – парабола. Так как сосуд обладает симметрией относительно оси Z, то любое другое осевое сечение этой фигуры также является параболой.

Установите при помощи поля численного ввода угловую скорость вращения сосуда и нажмите кнопку Старт. Убедитесь, что свободная поверхность жидкости в сосуде принимает форму параболоида. Управление анимацией осуществляется кнопками Стоп и Сброс.