Глава 3. Дифференцирование и интегрирование функций

3.1. Производная

3.1.2. Геометрический смысл производной

1

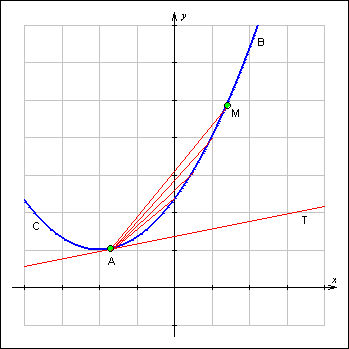
Рисунок 3.1.2.1. Определение касательной

Возьмем кривую CAB, выберем на ней точку M и проведем секущую AM. Будем приближать по дуге точку M к точке A. В этом случае прямая AM будет поворачиваться вокруг точки A, приближаясь (для гладких линий) к некоторому пределу – прямой AT. Другими словами Прямую AT, обладающую таким свойством, называют касательной к кривой CAB в точке A.

Угловой коэффициент секущей AM при AM → 0 стремится к угловому коэффициенту касательной AT: Данное равенство справедливо, если в точке A существует невертикальная касательная к кривой CAB.

Если кривая CAB является графиком функции f (x), то для углового коэффициента k касательной можно записать:
(здесь и далее x₀ и f (x₀) – координаты точки касания). Функция f (x) дифференцируема в точке x₀ тогда и только тогда, когда к графику функции в этой точке можно построить невертикальную касательную, причем угловой коэффициент этой касательной равен производной функции в этой точке:

Другими словами, производная функции в точке x₀ равняется тангенсу угла наклона касательной к графику функции в этой точке. Уравнение прямой, проходящей через точку (a; b), задается формулой y = k (x – a) + b. Поэтому уравнение касательной в общем случае выглядит так:

Проходящие через точку A прямые с угловыми коэффициентами и называются, соответственно, левой и правой касательными к графику функции y = f (x) в точке A. Эти касательные совпадают, если функция f дифференцируема в точке A.

Пусть графики функций y = f₁(x) и y = f₂(x) пересекаются в точке A. Углом φ между их графиками называется угол, образованный касательными к ним в точке A. В этом случае

Модель 3.2. Касательная и нормаль

Нормалью к графику функции y = f (x) в точке A (x₀; y₀) называется прямая, проходящая через точку A и перпендикулярная касательной к этой точке. Она задается уравнением
что следует из свойства угловых коэффициентов перпендикулярных друг другу прямых.

В случае бесконечной производной касательная в точке x₀ становится вертикальной и задается уравнением x = x₀, а нормаль – горизонтальной: y = y₀.