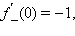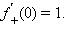Глава 3. Дифференцирование и интегрирование функций
3.1. Производная
3.1.1. Определение производной
Для решения многих задач требуется найти разность значений функции в двух точках. Так, средняя скорость материальной точки за промежуток времени Δt равна
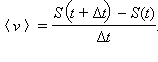 Если рассматриваемое движение не является равномерным, то чем меньше выбран промежуток времени Δt, тем лучше указанная формула будет характеризовать движение точки. В идеале мы получаем понятие мгновенной скорости v: это предел, к которому стремится средняя скорость, когда Δt → 0, то есть
Если рассматриваемое движение не является равномерным, то чем меньше выбран промежуток времени Δt, тем лучше указанная формула будет характеризовать движение точки. В идеале мы получаем понятие мгновенной скорости v: это предел, к которому стремится средняя скорость, когда Δt → 0, то есть
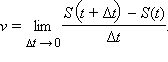
|
|
| График 3.1.1.1. Линеаризация функции y = sin x. |
Рассмотрим поведение графика функции y = sin x в окрестности точки x = 0. Если увеличивать масштаб графика, то кривизна графика становится все меньше и меньше, а сам график приближается к графику прямой y = x.
Эти и другие задачи приводят к понятию производной.
|
|
| График 3.1.1.2. К определению производной
|
Пусть функция y = f (x) определена в некоторой окрестности точки 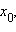 и существует конечный предел отношения
и существует конечный предел отношения
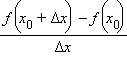 при Δx → 0. Тогда этот предел называется производной функции в точке
при Δx → 0. Тогда этот предел называется производной функции в точке 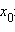
Производная функции y = f (x) может также обозначаться одним из следующих способов:
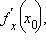
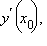
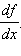 В физике производную по времени t часто обозначают точкой:
В физике производную по времени t часто обозначают точкой:
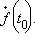
Если приращение функции f (x0 + Δx) – f (x0) обозначить как Δy, то определение можно записать так:
Из определения производной и предела функции следует, что
где α (Δx) – бесконечно малая функция при Δx → 0.
Операция вычисления производной называется дифференцированием. Функция называется дифференцируемой в данной точке, если в этой точке существует ее производная.

 |
|
Модель 3.1.
Дифференцирование функций
|
По аналогии с пределами вводится понятие правой и левой производных:
Если существует производная в точке 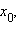 то существуют левая и правая производная в этой же точке, причем
то существуют левая и правая производная в этой же точке, причем
Обратное также верно: если
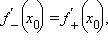 то производная
то производная
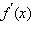 в точке
в точке 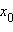 существует и равна левой и правой производным.
существует и равна левой и правой производным.
|
|
| График 3.1.1.3. Функция y = |x|1/2 имеет в точке x = 0 бесконечную производную неопределенного знака.
|
Можно ввести также понятие бесконечной производной
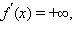

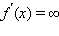 (последний случай может иметь место, если, например,
(последний случай может иметь место, если, например,
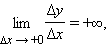 а
а
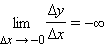 ).
).
Если функция дифференцируема в точке x0, то она непрерывна в этой точке.
Обратное, вообще говоря, неверно. Примером может служить функция y = |x|, непрерывная в точке x = 0, но имеющая в ней «излом». Производная этой функции в точке x = 0 не существует, так как
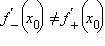 :
:
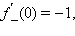
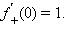






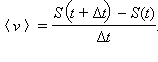
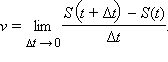
 и существует конечный предел отношения
и существует конечный предел отношения
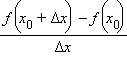
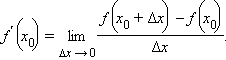
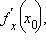
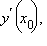
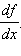
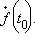
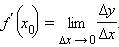
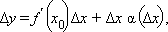


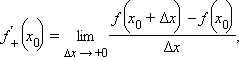
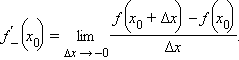
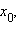 то существуют левая и правая производная в этой же точке, причем
то существуют левая и правая производная в этой же точке, причем
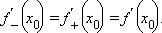
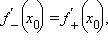
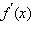
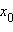 существует и равна левой и правой производным.
существует и равна левой и правой производным.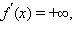

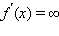
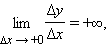 а
а
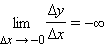 ).
).
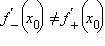 :
: