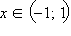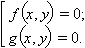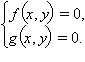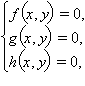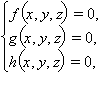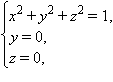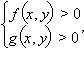Глава 2. Элементарные функции и их графики
2.5. Графические методы решения задач
2.5.3. Решение систем уравнений и неравенств
Уравнение g (x, y) = 0 задает на координатной плоскости некоторую кривую, каждая точка M (x; y) которой удовлетворяет этому уравнению.
Некоторые кривые являются графиками функций y = f (x), что означает равносильность уравнений g (x, y) = 0 и y = f (x). К таковым, например, относится кривая, задаваемая уравнениями x + y – 1 = 0 или y – x2 = 0. Другим не соответствуют никакие функции, например, 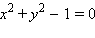 (в данном случае каждому значению
(в данном случае каждому значению
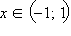 соответствуют два значения y).
соответствуют два значения y).
|
|
| График 2.5.3.1. Окружность с центром в точке (-2; 1).
|
|
|
| График 2.5.3.2. Гипербола, задаваемая уравнением x2 – y2 = 1.
|
Уравнением окружности с центром в точке (a; b) и радиусом r > 0 является
| (x – a)2 + (y – b)2 = r2. |
Уравнение (x – a)2 + (y – b)2 = 0 задает точку с координатами (a; b), уравнение x2 – y2 = a2 – гиперболу.
Уравнение вида
задает на плоскости объединение линий f (x, y) = 0 и g (x, y) = 0. Каждая точка этой фигуры является решением совокупности уравнений

 |
|
Модель 2.21.
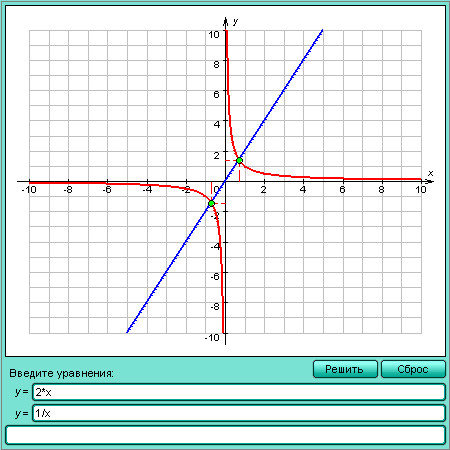
Система уравнений с двумя переменными
|
Пусть задана система уравнений
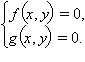 Ее решением является совокупность пар чисел (xi; yi), подстановка которых в каждое из уравнений превращает его в верное равенство. Построим на координатной плоскости кривые, задаваемые уравнениями f (x, y) = 0 и g (x, y) = 0. Тогда можно сказать, что геометрически решением системы уравнений является совокупность всех точек Mi (xi; yi), в которых пересекаются кривые, задаваемые этими уравнениями.
Ее решением является совокупность пар чисел (xi; yi), подстановка которых в каждое из уравнений превращает его в верное равенство. Построим на координатной плоскости кривые, задаваемые уравнениями f (x, y) = 0 и g (x, y) = 0. Тогда можно сказать, что геометрически решением системы уравнений является совокупность всех точек Mi (xi; yi), в которых пересекаются кривые, задаваемые этими уравнениями.
Если кривые не пересекаются, то система уравнений решений не имеет. В этом случае говорят, что система несовместна.
Систему
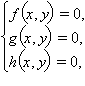 геометрически можно представить как совокупность точек, в которых пересекаются три кривые f (x, y) = 0, g (x, y) = 0 и h (x, y) = 0. Если не существует точки, в которой пересекаются все три кривые, то система также несовместна.
геометрически можно представить как совокупность точек, в которых пересекаются три кривые f (x, y) = 0, g (x, y) = 0 и h (x, y) = 0. Если не существует точки, в которой пересекаются все три кривые, то система также несовместна.
Аналогичным образом уравнение f (x, y, z) = 0 задает поверхность в трехмерной декартовой системе координат. Геометрически решением системы уравнений
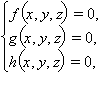 будет совокупность координат точек Mi (xi; yi; zi), в которых пересекаются поверхности, задаваемые этими уравнениями.
будет совокупность координат точек Mi (xi; yi; zi), в которых пересекаются поверхности, задаваемые этими уравнениями.
Так, уравнения x2 + y2 + z2 = 1, y = 0, z = 0 задают в пространстве сферу единичного радиуса с центром в начале координат и две координатные плоскости, перпендикулярные соответственно оси ординат и оси аппликат. Плоскость z = 0 пересекает сферу по окружности x2 + y2 = 1, лежащей в плоскости z = 0. Плоскость y = 0 пересекает эту окружность в двух точках с координатами M1 (–1; 0; 0) и M2 (1; 0; 0). Таким образом, решением системы уравнений
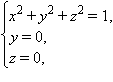 являются две тройки чисел (±1; 0; 0).
являются две тройки чисел (±1; 0; 0).
|
|
| График 2.5.3.3. Иногда при решении задач графики могут ввести в заблуждение. Так, на эскизе кажется, что графики функций y = (1/16)x и y = log1/16 x пересекаются только в одной точке, лежащей на биссектрисе первого координатного угла. И только при более внимательном рассмотрении у уравнения (1/16)x = log1/16 x находятся еще два корня x = 1/2 и x = 1/4. Увеличьте масштаб графика, чтобы убедиться в этом
|
Кривая f (x, y) = 0 делит координатную плоскость на несколько областей, внутри каждой из которых функция f сохраняет знак. Для решения неравенства
графическим методом необходимо в каждой из таких областей взять пробную точку и вычислить ее знак, после чего отобрать области, в которых функция f принимает положительные значения. Присоединяя к полученному решению саму кривую, получим решение неравенства
Чтобы решить графически систему
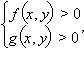 нужно изобразить на координатной плоскости решения каждого из неравенств f (x, y) > 0, g (x, y) > 0, а затем найти их пересечение. Аналогичным образом поступают, если неравенств больше двух.
нужно изобразить на координатной плоскости решения каждого из неравенств f (x, y) > 0, g (x, y) > 0, а затем найти их пересечение. Аналогичным образом поступают, если неравенств больше двух.






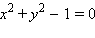 (в данном случае каждому значению
(в данном случае каждому значению