Глава 1. Электродинамика

Задачи с решениямиЗадачи с решениямиВключить/Выключить фоновую музыкуВключить/Выключить звуки событий


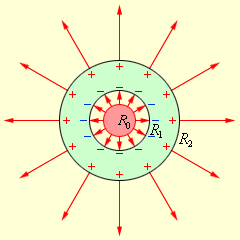Во сколько раз изменится потенциал заряженного проводящего шара радиусом R0 = 5 см, если поместить его в центр толстостенной проводящей незаряженной сферической оболочки с внутренним радиусом R1 = 10 см и наружным R2 = 20 см?

Решение

Задача обладает сферической симметрией. Из теоремы Гаусса следует, что электрическое поле в пространстве между заряженным шаром и оболочкой, а также вне оболочки остается неизменным. Внутри проводящей оболочки напряженность электрического поля обращается в нуль. На внутренней и внешней сферических поверхностях оболочки возникают индуцированные заряды (см. рис.).

В отсутствие сферической оболочки потенциал заряженного шара равен

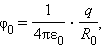
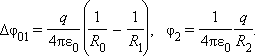
где q – заряд шара. При наличии оболочки потенциал φ1 шара равен сумме Δφ01 + φ2, где Δφ01 – разность потенциалов между шаром и проводящей оболочкой, φ2 – потенциал оболочки.

Из этих соотношений следует


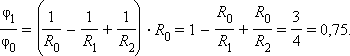
 2 из 2