Глава 2. Электромагнитные колебания и волны Задачи с решениями
Задачи с решениями

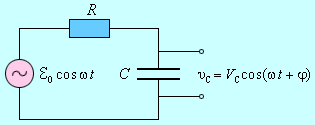
Конденсатор емкостью C = 1,0 мкФ последовательно с резистором сопротивлением R = 5 кОм подключен к генератору переменного напряжения  =
=  0 cos ωt (см. рис.). Круговая частота ω = 200 с–1. Определите:
0 cos ωt (см. рис.). Круговая частота ω = 200 с–1. Определите:
1) отношение V0 /  0 амплитуды V0 напряжения на конденсаторе к амплитуде
0 амплитуды V0 напряжения на конденсаторе к амплитуде  0 напряжения генератора;
0 напряжения генератора;
2) сдвиг фаз между напряжением генератора и напряжением на конденсаторе.
РешениеЗапишем закон Ома для цепи переменного тока:
Здесь J и V – мгновенные значения тока в цепи и напряжение на конденсаторе. Принимая во внимание, что 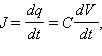 где q – заряд конденсатора, получим
где q – заряд конденсатора, получим
Мы получили линейное дифференциальное уравнение, описывающее процессы, происходящие в RC-цепях под действием синусоидального напряжения генератора. Будем искать решение в виде V = V0 cos (ωt + φ). Подставим это выражение в дифференциальное уравнение:
Полученное трансцендентное уравнение проще всего решать графически с помощью векторной диаграммы. Первый член этого уравнения по формулам тригонометрии можно преобразовать к виду:
–ωRCV0 sin (ωt + φ) = ωRCV0 cos (ωt + φ + π / 2).
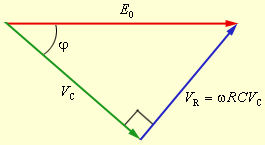
Отсюда следует, что колебания, описываемые первым и вторым членами в левой части уравнения, сдвинуты по фазе на угол π / 2. На векторной диаграмме эти колебания должны изображаться векторами, ориентированными перпендикулярно друг другу, и, следовательно, векторная диаграмма должна иметь вид прямоугольного треугольника (см. рис.).
-
Из данных в условии задачи следует, что ωRC = 1, следовательно
-
Фазовый сдвиг φ между напряжением генератора и напряжением на конденсаторе определяется соотношением
tg φ = – ωRC = –1.
φ = – π / 4.
Напряжение на конденсаторе отстает по фазе от напряжения генератора на угол π / 4.
 1 из 2
1 из 2
 |


 Задачи с решениями
Задачи с решениями

![]() =
= ![]() 0
0![]()
![]()
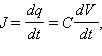 где
где 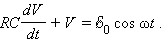
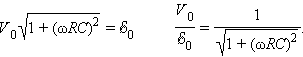
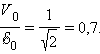
 1 из 2
1 из 2
