

 Задачи с решениями
Задачи с решениями

Одну из серий экспериментов по измерению скорости света Майкельсон проводил на базе
Сколько времени потребуется свету, чтобы пройти расстояние
Предположим, что база
Принимая для скорости света значение

Рассмотрим распространение света на базе
 |
На пути от источника
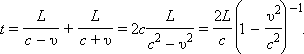
Так как  выражение
выражение 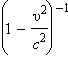 можно разложить в ряд по биноминальному закону. Это дает
можно разложить в ряд по биноминальному закону. Это дает

Окончательно выражение для
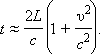
Отсюда следует, что классическая поправка
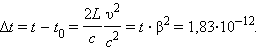
Здесь принято обозначение
 1 из 2
1 из 2
 |