Декартовы координаты Задачи с решениями
Задачи с решениями

Проанализировать взаимное расположение прямых a1x + b1y + c1 = 0, a2x + b2y + c2 = 0.
Решение
Ввиду замечания к доказательству теоремы 11.5 эти уравнения определяют прямые, если a12 + b12 > 0, a22 + b22 > 0. Пусть для определенности 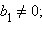 выразим y из первого уравнения и подставим во второе:
выразим y из первого уравнения и подставим во второе:
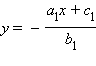 и
и
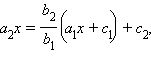
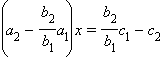 или
или 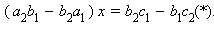 Пусть
Пусть 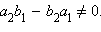 Тогда решение последнего уравнения единственно, и
Тогда решение последнего уравнения единственно, и
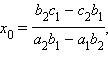 и далее
и далее
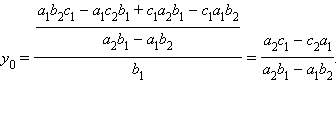 Таким образом, при условии, что a2b1 – a1b2 ≠ 0, существует единственная точка A(x0; y0), координаты которой удовлетворяют обоим уравнениям, и, следовательно, эти прямые пересекаются в точке А. Пусть теперь
Таким образом, при условии, что a2b1 – a1b2 ≠ 0, существует единственная точка A(x0; y0), координаты которой удовлетворяют обоим уравнениям, и, следовательно, эти прямые пересекаются в точке А. Пусть теперь 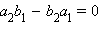 Это значит,
Это значит,
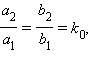 если
если 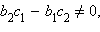 т. е.
т. е.
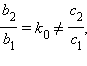 то никакое число x не является решением уравнения (*), и, следовательно, исходные уравнения не имеют общих решений. Это значит, что прямые не пересекаются, т. е. они параллельны. Таким образом, мы получили следующий признак параллельности двух прямых, заданных исходными уравнениями. Если коэффициенты при переменных пропорциональны, т. е.
то никакое число x не является решением уравнения (*), и, следовательно, исходные уравнения не имеют общих решений. Это значит, что прямые не пересекаются, т. е. они параллельны. Таким образом, мы получили следующий признак параллельности двух прямых, заданных исходными уравнениями. Если коэффициенты при переменных пропорциональны, т. е.
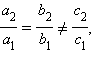 а отношение свободных коэффициентов не равно отношению соответствующих коэффициентов, то уравнения определяют параллельные прямые. Пусть теперь
а отношение свободных коэффициентов не равно отношению соответствующих коэффициентов, то уравнения определяют параллельные прямые. Пусть теперь
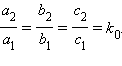 Тогда любая точка x – является решением уравнения (*) и в силу произвольности x связь между x и y определяется одним из исходных уравнений, потому что другое уравнение пропорционально первому. В этом случае каждое уравнение совокупности исходных уравнений задает одну и ту же прямую.
Тогда любая точка x – является решением уравнения (*) и в силу произвольности x связь между x и y определяется одним из исходных уравнений, потому что другое уравнение пропорционально первому. В этом случае каждое уравнение совокупности исходных уравнений задает одну и ту же прямую.
 1 из 24
1 из 24
 |


 Задачи с решениями
Задачи с решениями

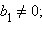 выразим
выразим 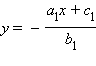 и
и
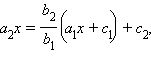
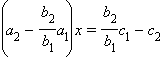 или
или 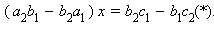 Пусть
Пусть 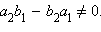 Тогда решение последнего уравнения единственно, и
Тогда решение последнего уравнения единственно, и
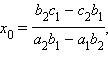 и далее
и далее
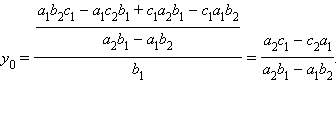 Таким образом, при условии, что
Таким образом, при условии, что 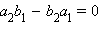 Это значит,
Это значит,
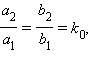 если
если 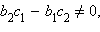 т. е.
т. е.
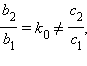 то никакое число
то никакое число 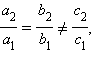 а отношение свободных коэффициентов не равно отношению соответствующих коэффициентов, то уравнения определяют параллельные прямые. Пусть теперь
а отношение свободных коэффициентов не равно отношению соответствующих коэффициентов, то уравнения определяют параллельные прямые. Пусть теперь
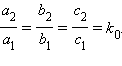 Тогда любая точка
Тогда любая точка  1 из 24
1 из 24
