Декартовы координаты Задачи с решениями
Задачи с решениями

Проанализировать взаимное расположение окружности и прямой.
Решение
Пусть w (O; R) – данная окружность, ax + by + c = 0, b ≠ 0 – данная прямая, d – расстояние от центра окружности до прямой. Примем центр окружности за начало координат, а прямую, перпендикулярную данной прямой, за ось OX. Тогда уравнение окружности имеет вид x2 + y2 = R2, а уравнение прямой – x = d. Для того чтобы прямая и окружность пересекались, необходимо и достаточно, чтобы система двух уравнений имела общее решение. Решая систему имеем: x = d,
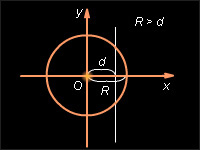
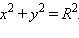 Отсюда, если d < R, то прямая и окружность имеют две точки пересечения (см. первый рисунок); если d = R, то прямая и окружность касаются (см. второй рисунок); если d > R, то система не имеет решений, то есть прямая и окружность не пересекаются (см. третий рисунок).
Отсюда, если d < R, то прямая и окружность имеют две точки пересечения (см. первый рисунок); если d = R, то прямая и окружность касаются (см. второй рисунок); если d > R, то система не имеет решений, то есть прямая и окружность не пересекаются (см. третий рисунок).
|
Прямая и окружность имеют две точки пересечения.
|
|
|
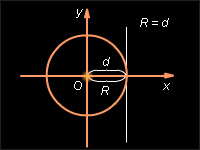
Прямая и окружность касаются.
|
|
|
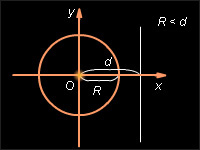
Прямая и окружность не пересекаются.
|
|
 2 из 24
2 из 24
 |


 Задачи с решениями
Задачи с решениями

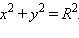 Отсюда, если
Отсюда, если  2 из 24
2 из 24
