Декартовы координаты Задачи с решениями
Задачи с решениями

Вычислить коэффициенты a, b, c уравнения прямой, проходящей через две заданные точки:
а) A1(1; 2) и A2(0; 1);
б) A1(1; 2) и A2(1; 3);
в) A1(1; 2) и A2(0; 2).
Решение
По теореме 11.5 уравнение прямой имеет вид ax + by + c = 0, а координаты точек A1 и A2 одновременно удовлетворяют этому уравнению.
а) Имеем: 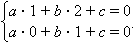 Вычтем второе равенство из первого и получим a + b(2 – 1) = 0; или a + b = 0; выразим a через b и подставим в исходное уравнение прямой. a = b = 0 не удовлетворяет полученному равенству, так как в этом случае исходное уравнение не задает прямой. Получим –bx + by + c = 0. Поделив на b и обозначив
Вычтем второе равенство из первого и получим a + b(2 – 1) = 0; или a + b = 0; выразим a через b и подставим в исходное уравнение прямой. a = b = 0 не удовлетворяет полученному равенству, так как в этом случае исходное уравнение не задает прямой. Получим –bx + by + c = 0. Поделив на b и обозначив
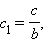 получим
получим 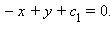 Чтобы найти c1, подставим в уравнение координаты одной из точек, например, A2 и получим –0 + 1 + c1 = 0; c1 = –1. Окончательно получим: -x + y – 1 = 0 – уравнение исходной прямой. Действительно, координаты точек A1и A2 удовлетворяют данному уравнению, а в соответствии с аксиомой 2.2 через две разные точки A1 и A2 можно провести единственную прямую.
Чтобы найти c1, подставим в уравнение координаты одной из точек, например, A2 и получим –0 + 1 + c1 = 0; c1 = –1. Окончательно получим: -x + y – 1 = 0 – уравнение исходной прямой. Действительно, координаты точек A1и A2 удовлетворяют данному уравнению, а в соответствии с аксиомой 2.2 через две разные точки A1 и A2 можно провести единственную прямую.
б) Аналогично запишем систему равенств, подставив в уравнение прямой значения координат точек A1(1; 2) и A2(1; 3): 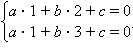 Вычтя первое равенство из второго, имеем b = 0. Как следствие, a ≠ 0. Имеем ax + c = 0, или
Вычтя первое равенство из второго, имеем b = 0. Как следствие, a ≠ 0. Имеем ax + c = 0, или
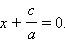 Обозначив
Обозначив
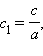 получим вид уравнения
получим вид уравнения 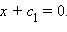 Подставим значение координат точки
Подставим значение координат точки 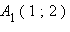 в данное уравнение: 1 + c1 = 0; c1 = –1. Окончательно x – 1 = 0.
в данное уравнение: 1 + c1 = 0; c1 = –1. Окончательно x – 1 = 0.
в) Запишем систему равенств
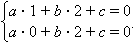 Как следствие, имеем a = 0, b ≠ 0. Следовательно, уравнение прямой имеет вид y + c1 = 0. Находим c1, подставив координаты (0; 2) точки A2. Уравнение прямой имеет вид y – 2 = 0.
Как следствие, имеем a = 0, b ≠ 0. Следовательно, уравнение прямой имеет вид y + c1 = 0. Находим c1, подставив координаты (0; 2) точки A2. Уравнение прямой имеет вид y – 2 = 0.
 3 из 24
3 из 24
 |


 Задачи с решениями
Задачи с решениями

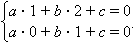 Вычтем второе равенство из первого и получим
Вычтем второе равенство из первого и получим 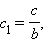 получим
получим 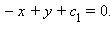 Чтобы найти
Чтобы найти 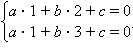 Вычтя первое равенство из второго, имеем
Вычтя первое равенство из второго, имеем 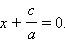 Обозначив
Обозначив
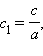 получим вид уравнения
получим вид уравнения 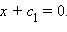 Подставим значение координат точки
Подставим значение координат точки 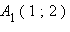 в данное уравнение:
в данное уравнение: 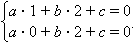 Как следствие, имеем
Как следствие, имеем  3 из 24
3 из 24
