Декартовы координаты Задачи с решениями
Задачи с решениями

Найти вид уравнения прямой, перпендикулярной данной.
Решение
Пусть ax + by + c = 0 – уравнение данной прямой, а a1x + b1y + c1 = 0 – уравнение прямой, перпендикулярной к данной.
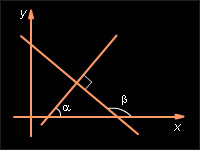
а) Пусть b ≠ 0, a ≠ 0. Тогда b1 ≠ 0, a1 ≠ 0. В противном случае, если b1 = 0, прямая a1x + c1 = 0 параллельна оси Oy, если a1 = 0, прямая b1y + c1 = 0 параллельна оси OX. В обоих случаях нарушается условие перпендикулярности прямых. Уравнение прямых в этом случае можно переписать в виде y = kx + d; 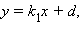 где
где 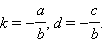 Как известно, k = tg α,
Как известно, k = tg α, 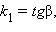
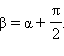
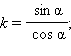
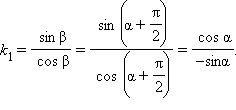 Поэтому
Поэтому 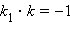 и уравнение прямой, перпендикулярной к данной, имеет вид
и уравнение прямой, перпендикулярной к данной, имеет вид 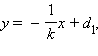 или
или
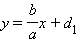 и
и 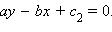
б) b = 0. Как известно, данное уравнение ax + c = 0 параллельно оси OY. Следовательно, ортогональная прямая параллельна оси OX и ее уравнение имеет вид b1y + c1 = 0, b1 ≠ 0. Умножив члены уравнения на число
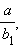 имеем ay + c2 = 0.
имеем ay + c2 = 0.
в) a = 0. Аналогично получаем уравнение исходной прямой by + c = 0, ортогональная ей прямая имеет уравнение a1x + c1 = 0. a1 ≠ 0 и после умножения на
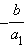 получим –bx + c2 = 0. Следовательно, пункты б) и в) получаются как частный случай пункта а).
получим –bx + c2 = 0. Следовательно, пункты б) и в) получаются как частный случай пункта а).
 4 из 24
4 из 24
 |


 Задачи с решениями
Задачи с решениями

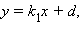 где
где 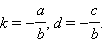 Как известно,
Как известно, 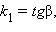
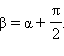
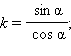
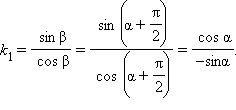 Поэтому
Поэтому 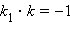 и уравнение прямой, перпендикулярной к данной, имеет вид
и уравнение прямой, перпендикулярной к данной, имеет вид 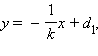 или
или
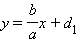 и
и 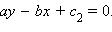
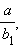 имеем
имеем 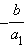 получим
получим  4 из 24
4 из 24
